Grafikus adatmodellek I
Ebben a részben megismerkedünk:
fogalom vázlatával, és megkezdjük a vektoros adatmodellek részletes tárgyalását, ezen belül bemutatjuk a sphagetti módszert.
A térbeli információs rendszerek egyik legáltalánosabb tulajdonsága, hogy két különböző fajta adattípust (a grafikust és alfanumerikust), vagy logikai oldalról megközelítve, a hely és tulajdonság jellemzőket, egységes rendszerben tárolják és kezelik.
Az előző részekben ismertetett adatbanki rendszereket az alfanumerikus adatok tárolására és kezelésére dolgozták ki. A fejlődés során a különböző adatmodelleken és szervezési elveken nyugvó adatbáziskezelő rendszerek közül a relációs adatbáziskezelő rendszerek szerezték meg a győzelmet.
A grafikus (helyleíró) adatok olyan speciális tulajdonságokkal rendelkeznek, melyek figyelembe vétele jelentősen csökkenti az igénybe veendő tárkapacitást, és egyszerűsíti a végrehajtandó műveleteket. A grafikus adatok ugyanakkor nem igényelnek sok olyan műveletet illetve kapcsolatot, melyek megléte az alfanumerikus adatbáziskezelő rendszerekben meghatározó. Ez az oka annak, hogy a jelenleg működő térinformatikai rendszer (LIS, GIS) szoftverek jelentős része, legalább ideiglenesen, külön adatbázisban tárolja a grafikus adatokat és egy másik, rendszerint relációs adatbázisban, az alfanumerikus adatokat. A két adatbázis közötti kommunikációról egy kapcsoló szoftver rendszer gondoskodik.
Mivel napjainkban a hardverkötöttségek jelentősége egyre inkább csökken (mind a tárkapacitás, mind a műveleti sebességek rohamosan nőnek), újabban olyan szoftvereket is találhatunk már, melyek a két fajta adatállományt közös relációs adatbázisban kezelik. Ezeknél a megoldásoknál speciális szoftvermodul gondoskodik arról, hogy a grafikus adatok a jellegükből következő egyszerűsítési lehetőségek kihasználásával kerüljenek ideiglenes tárolásra és manipulálásra.
A legújabb irányzatok, ma még csak egy kereskedelmi szoftverben, az objektum orientált programozásból kiindulva, objektum orientált adatbázisokat kívánnak létrehozni a térbeli adatoknak.
A helyleíró adatok hagyományos ábrázolási formája a vektor modell. A tárolás alapeleme ebben a megközelítésben a vonaldarab. Ez a modell mindannyiunk számára közeli, hisz geometriai, geodéziai, (manuális) térképezési módszereink mind ezt az alapelvet követik. A terep vektoros ábrázolása azonban csak jelentős egyszerűsitő munka eredményeképpen jöhet létre, hisz a terep minden pontja önálló, a többi ponttól eltérő sajátosságokkal is rendelkezhet.
Az absztrakció egy alacsonyabb szintjén kézenfekvő, hogy a terep képét kis, homogén területekre osztjuk és az így kapott területeket tároljuk illetve manipuláljuk. A valóság képét területelemekben rögzítő módszereket tesszellácionak nevezzük. Azon az alapon, hogy milyen az elemi területek alakja szabályos és szabálytalan tesszellációról beszélünk. A szabályos tesszelláció általában hierarchikus struktúrába szervezhető, azaz a kisebb területekből szakadásmentesen hasonló alakú nagyobb területek hozhatók létre.
A tesszellációs modell elterjedése kapcsolatban van azzal a ténnyel is, hogy a korszerű grafikus képernyők mind raszter grafikával dolgoznak, azaz függetlenül az adatbázisban alkalmazott grafikus adatmodelltől a megjelenítés mindig raszteres lesz (ezért néznek ki az alacsony felbontású monitorokon a nem függőleges vagy vizszintes vonalak fűrészfogszerűen).
A raszteres modell a tesszellációs modellnek az a legelterjedtebb változata, amelyben a területegység a négyzet. A továbbiakban elsősorban a raszteres modellt fogjuk tárgyalni.
Másik oka a raszteres modellek terjedésének abban rejlik, hogy a volumenben legjelentősebb adatnyerő eszközök (műholdas érzékelő és továbbitó rendszerek, digitalizált, vagy digitális kamarával készült légifényképek, scanneres technikával digitalizált térképek) mind raszteres termékeket szolgáltatnak. Ebből következik, hogy még akkor is, ha egy térinformatikai szoftver vektoros adatmodellt alkalmaz, célszerű ha rendelkezik olyan programmodulokkal, melyek a raszteres bemenő adatok fogadását, illetve a raszteres megjelenítést lehetővé teszik.
A grafikus adatmodell kialakításánál két alapvető szempont játssza a főszerepet: mennyire tömöríthető a modellben az információ, illetve hogyan hat a (tömöritett) modell a műveleti sebességre. A két követelmény együttesen sohasem elégíthető ki optimálisan, ezért rendszerint az adott hardver-feltételekhez legjobban illő kompromisszum szolgáltatja a megoldást.
A valódi térbeli háromdimenziós számítógépes testábrázolás először a gépészeti tervező rendszerekben jelent meg. Itt is megtaláljuk a vektoros és tesszellációs módszerek megfelelőit ezek a határleírás módszere illetve a konstruktív test geometria.
A bányászati-földtani rendszerekben, amelyekben a legfőbb probléma az információ hiány (rendszerint szórt, pontszerű információ áll csak rendelkezésre) a tesszellációs módszerek, mind a szabálytalan, mind a szabályos, játszzák a döntő szerepet. A tesszeláció alapegysége ebben az esetben egy elemi test, a szabálytalan tesszellációban ez vagy egy tetraéder vagy egy Voronoi poliéder, a szabályos tesszellációban pedig egy kocka.
Az elemi testekkel homogén vagy annak tekinthető alakzatokat (pld. érctelér, üreg) írhatunk le. Sok esetben azonban az alakzat bizonyos paraméterek szempontjából nem tekinthető homogénnek. Ilyenkor a paraméterek alakzaton belüli változását különböző interpolációs módszerek alkalmazásával modellezhetjük. Ezeket az eljárásokat közös névvel skalár terek modellezésének hívják.
Vektoros modellek
A vektoros modellek lényege, hogy az ábrázolandó területet és a rajta lévő objektumokat pontok és a köztük lévő egyenesek együtteseként fogja fel. Ezen az elven az sem változtat, hogy a legtöbb rendszer alkalmas szabályos ívek generálására is a pontok között, mivel az ívek is elképzelhetőek differenciálisan kicsiny egyenes darabokból (húrokból) alkotott poligonokként.
A terep absztrakciója következtében a térképen, így a digitális térképen is pontszerű, vonalas és területi objektumok találhatók.
A pontszerű objektumokat
a vektoros modell alap meghatározását alkalmazva úgy értelmezzük, mint egy olyan nulla hosszúságú egyenest, melynek kezdő és végpontja azonos.
A vonalszerű objektumok,
mint egyenesek folytonos mondatai értelmezhetők,
a területi
objektumok
explicit értelmezéséhez és különösen a területekkel való folytonos lefedéshez még tovább kell fejleszteni modellünket bizonyos topológiai meggondolásokkal.
Sphagetti módszer
A módszert a digitális térképezés kezdetén alkalmazták, napjainkban már inkább csak történelmi, módszertani jelentősége van.
Lényege az, hogy minden egyes vonalas objektumot egy a vonal töréspontok koordinátáiból álló sorozat (adatmondat vagy sztring) ábrázol a gép memóriájában.
A módszernek több hátránya van, a legnagyobb az, hogy a koordináták keresése szekvenciális s ez lelassítja a műveleteket különösen a szerkesztési-javítási eljárásokat. A másik probléma a területek digitalizálásánál lép fel.
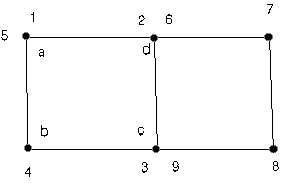
2.1 ábra - digitalizálási sorrend a sphagetti modell alkalmazásakor
Képzeljük el, hogy a
2.1 ábrán látható telkeket akarjuk kézi úton ledigitalizálni. A digitalizálást
a számokkal jelölt sorrendben hajtjuk végre. Az első adatmondat az 5 ponttal
végződik. Ahhoz, hogy az 1 és 5 pontok koordinátái azonosak legyenek külön
adatmondat típust kell beilleszteni a rendszerbe, s ezzel az eredeti egyszerű
modellel szemben egy fejlesztett modellt alkalmazni. Még ez a bővítés sem oldja
meg azonban a két poligon csatlakozását (azaz a 2 és 6 valamint a 3 és 9
egybeesését) hisz a két poligon külön külön adatmondatokban van tárolva és
olyan algoritmus megkonstruálása, mely a különböző adatmondatokban lévő de
egymáshoz túl közel fekvő pontokat kiválogatja és egybeolvasztja igen bonyolult
és nem kecsegtet gyors és egyértelmű megoldással.
Másik nehezen
megoldható probléma a modellben az egymást metsző vonalas objektumok
metszéspontainak meghatározása.
Végül előnytelen a
módszer a redundancia szempontjából is hisz példánk esetében a b pont
koordinátáit két adatmondatban összesen háromszor (az elsőben egyszer a
másodikban kétszer) kell tárolnunk.
ˇ a következő részben folytatjuk a vektoros modellek ismertetését,
ˇ visszatérhet az előző részhez is,
ˇ vagy a tartalomjegyzékhez.
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc