Grafikus adatmodellek II

Ebben a részben megismerkedünk:

  1. a topológiai modellel és
  2. a háló modellel.

Topológiai modell

A topológia egy olyan matematikai tudomány, mely bizonyos geometriai tulajdonságokból kiindulva, azok általánosítása alapján, algebrai törvényszerűségeket határoz meg. A geometriai topológia a téralakzatok azon tulajdonságait vizsgálja, melyek nem változnak az idomok szakadásmentes torzítása során. Ilyenek a szomszédság, folyamatosság, tartalmazás. A 2.2 ábra topológiailag hasonló alakzatokat mutat be.

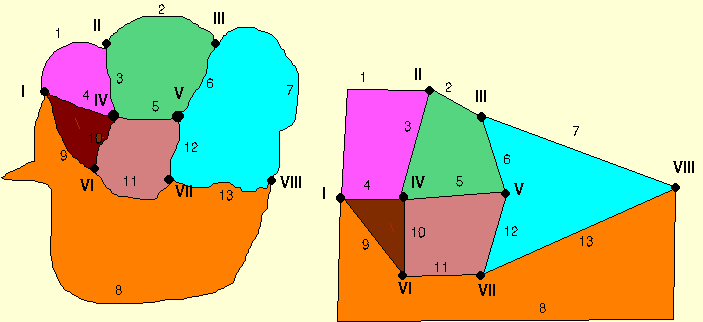
2.2 ábra - topológiailag hasonló alakzatok

Míg a sphagetti modell csak vonaldarabokkal operál, a topológiai modell a topológiai törvényszerűségek kiaknázását lehetővé tevő adat típusokat is értelmez. Bár a topológiai modell is metrikus térben helyezkedik el, melynek alapja a koordinátás pontok halmaza s a köztük definiált távolság fogalom, a pontok a topológiai struktúra felépítésében játszott szerepük alapján különböző típusokra oszthatók, ezek:

  1. önálló pont;
  2. lánc (ív) részét képező pont;
  3. csomópont.

Az önálló pont a valóság modellezése során kapott olyan objektumok leírására szolgál, melyek területi kiterjedése elhanyagolható. Ilyen objektumok lehetnek a kutak, források, geodéziai alappontok, tv-, vagy rádióadó antennák, hidroglóbuszok, kémények, vezetéktartó oszlopok stb.

A terepi objektumok egy másik csoportja vonalakkal modellezhető, ilyenek a vízfolyások, utak, vasutak, csővezetékek, föld alatti és föld feletti kábelek stb. A vonalas objektumok töréspontokat tartalmaznak, melyek valamely (általában lineáris) törvényszerűségen alapuló összekötése szolgáltatja a vonalas objektumot. Míg azonban a sphagetti modellben a vonalat alkotó pontok egyenrangúak, addig a topológiai modell a vonalakban kétféle ponttípust különböztet meg: a láncolatot (ívet) alkotó töréspontot és a csomópontot.

A töréspontok valamely egymásutánja alkotja a láncot, mely mindig két csomópont között helyezkedik el és az egyik csomópontról a másikra mutat, azaz a lánc irányított. A csomópontok a láncok végein helyezkednek el, ez vagy abból adódik, hogy a vonalas objektumnak a csomópontban vége van, vagy abból, hogy a csomópontban az objektum elágazik, vagy más vonalas objektummal metsződik. Következésképpen egy vonalas objektum általában kettőnél több csomópontot is tartalmaz.

Az objektumok egy jelentős száma, pld. a kataszteri rendszerek alapobjektumai, területi kiterjedésűek és folyamatosan borítják be a felszínt. Ezeknél az objektumoknál egy a hierarchia magasabb színtjén álló alapobjektum a poligon (zárt sokszög) felvétele látszik célszerűnek. A poligont az azt alkotó láncok meghatározott egymásutánja egyértelműen leírja.

Mivel folyamatos területlefedés esetén egy-egy lánc egyidejűleg két poligonnak is része, értelmezhető a lánc leírásánál, irányítottságának megfelelően, a jobboldali illetve baloldali poligon fogalma is. Az irányított láncok eredményesen alkalmazhatók az u.n. szigetek kezelésénél (2.3 ábra).

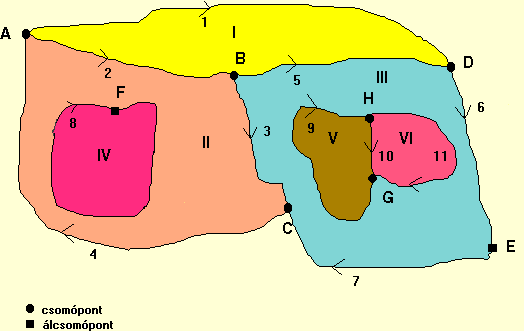
2.3 ábra - irányított láncokból (ívekből) felépített zárt sokszögek (poligonok)

A szigetek kezelése azt jelenti, hogy a befoglaló poligon területéből a területszámítás során a sziget területét le kell vonni.

Először azt kell megállapítani, hogy található-e az adott poligonon belül sziget. Ez a 2.3 ábra II poligonja esetében viszonylag egyszerűen elvégezhető mivel a szigeteként jelentkező IV poligont csak egy lánc alkotja, melynek baloldali poligonja II, jobboldali poligonja pedig IV. Ez azonban másképpen nem lehet csak úgy, hogy a IV poligon sziget a II-ben. Bonyolultabb a helyzet a III poligon V és VI poligonokból álló összetett szigete esetében. Itt a sziget meglétét úgy dokumentálhatjuk, hogy keresünk egy olyan összefüggő, önmagában záródó láncsorozatot, melynek baloldali poligonja a III. A dokumentálandó sziget az ehhez a lánc együtteshez tartozó jobboldali poligonokból fog állni, azaz példánk esetén az V és VI poligonból. Megjegyezzük, hogy az olyan csomópontokat, melyekből nincs elágazás, ilyenek a 2.3 ábrán E és F, álcsomópontoknak hívjuk. Míg az F álcsomópont létrehozása indokolt volt, nélküle az egy láncból álló zárt poligon nem értelmezhető, addig az E tipusú álcsomópont létrejöttét rendszerint digitalizálási hiba okozza, megléte érdemben nem befolyásolja a legtöbb szoftver munkáját, legföljebb egy kicsit növeli a futásidőt.

A topológiai modell fő előnyei a sphagetti modellel szemben elsősorban a tárolás, lekérdezés és karbantartás területén jelentkeznek. Ennek illusztrálására nézzük meg, hogy az alábbi egyszerű poligon rendszert hogyan tárolja egy topológiai struktúrájú micro GIS szoftver (2.4 ábra).

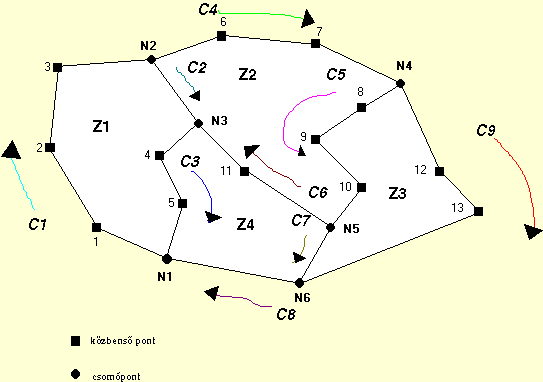
2.4 ábra - micro GIS topológiai modell minta alakzata

A vázlat elemzése előtt megjegyezzük, hogy a szoftverek rendszerint csak a csomópontok és koordinátáik, a töréspontok és koordinátáik bevitelét igénylik a felhasználóktól, a táblázatok összeállitásához szükséges többi adatot automatikusan állitják elő. Amennyiben a poligonok azonosításával kapcsolatban a felhasználónak különleges igényei vannak, úgy természetesen azokat is be kell vinni.

I. csomópontok

p.sz.

x

y

N1

x1

y1

N2

x2

y2

N3

x3

y3

N4

x4

y4

N5

x5

y5

N6

x6

y6

II. láncok

l. sz.

N1

N2

FP

NP

DC

C1

1

2

1

3

2

C2

2

3

0

0

1

C3

3

1

4

2

1

C4

2

4

6

2

2

C5

4

5

8

3

1

C6

5

3

11

1

1

C7

5

6

0

0

1

C8

6

1

0

0

2

C9

4

6

12

2

2

III. közbenső pontok

p.sz.

x

y

P1

x1

y1

P2

x2

y2

P3

x3

y3

P4

x4

y4

P5

x5

y5

P6

x6

y6

P7

x7

y7

P8

x8

y8

P9

x9

y9

P10

x10

y10

P11

x11

y11

P12

x12

y12

P13

x13

y13

IV. poligonok

pol.sz.

C1

NC

Z1

1

3

Z2

4

4

Z3

8

3

Z4

11

4

V. pointerek

p.s.sz.

PC

1

1

2

2

3

3

4

-2

5

4

6

5

7

6

8

-5

9

9

10

-7

11

-3

12

-6

13

7

14

8

láncok

N1: pointer a kezdő csomópontra

N2: pointer a végső csomópontra

FP: pointer az első közbenső

NP: közbenső pontok száma

DC: rajzoló kód

poligonok

C1: pointer az első láncpointerre

NC: a poligont alkotó láncok száma

PC: pointer a láncra

-: olyan lánc amit a rögzîtéssel ellentétes irányban kell olvasni

2.1 táblázat - micro GIS topológiai modell tárolási struktúrája

Az ábra és a 2.1 táblázat tanulsága szerint a topológiát három táblázat (II, IV, V) tartalmazza.

A II táblázat a láncokat definiálja olymódon, hogy megadja melyik csomópontból indul, s melyikbe érkezik a lánc, melyik az első közbenső pontja, s hány közbenső pontja van. Ez a megadás csak akkor kielégítő, ha a közbenső pontok koordinátái a III táblázatban a láncok irányítottságának megfelelő sorrendben helyezkednek el. Az utolsó oszlopban található "rajzi kódnak" a topológiához csak akkor van köze, ha segítségével, mint esetünkben, egyszerűen kiválaszthatók a burkoló poligont alkotó láncok.

A poligonok felépítését a IV, V és II táblázat együttesen szolgálja. Első ránézésre nem mindenki számára világos az V táblázat szerepe. Egyesek úgy gondolkodnak, hogy elég volna megadni a poligont alkotó első láncot és az alkotó láncok számát, s ezen adatok birtokában a II táblázatból a poligon felépíthető lenne. Ebben a gondolatmenetben az a hiba, hogy egy-egy lánc két poligonban is szerepel, s fölösleges helyfoglalás volna minden megjelenését beírni a II táblázatba. E helyett az V táblázatban mindössze két számmal hivatkozhatunk a kérdéses láncokra.

Végül, gyakorlásképpen nézzük meg, hogyan lehet a táblázatok felhasználásával meghatározni például a Z4 poligon területét.

A IV táblázatból a program megkeresi a Z4-es sort. A poligon azonosító utáni első mezőtartalom (11) arra utal, hogy az V táblázat 11. sorában van az a pointer (esetünkben -3), mely a II táblázatban a Z4 poligont alkotó első láncra C3-ra mutat. Mivel azonban a pointer előjele negatív a láncot fordított haladási értelemben kell figyelembe venni a területszámításhoz szükséges koordináta táblázat összeállításakor, azaz először az I táblázatból az N1 koordinátáit majd a II táblázatból a P5 és P4 töréspontokét, végül ismét az I táblázatból az N3 csomópont koordinátáit vesszük ki. Mivel a IV táblázat negyedik sora második mezejének tartalma 4, az eljárást még háromszor meg kell ismételni az V táblázat 12, 13 és 14 sorszámú pointereivel. A terület számító program készítésénél ügyelni kell arra, hogy a -3 lánc végső csomópontja (N3) azonos a -6 lánc kezdő csomópontjával, ezért koordinátáit a táblázatba csak egyszer kell behívni.

Amint láttuk a topológiai struktúra közvetlen lehetőséget biztosít vonalas objektumok, felületi objektumok összeállítására, illetve az utóbbiak esetében a szomszédos objektumok meghatározására is.

Még egy gyakran előforduló kérdésre lehet a topológiai modell segítségével választ adni: benne van-e egy adott pont egy poligonban (például egy ponttal jellemzett artézi kút a vizsgált földrészleten belül vagy kívül helyezkedik-e el)?

A választ szolgáltató algoritmus, mivel topológiai törvényszerűségeket tükröz, független a poligon alakjától.

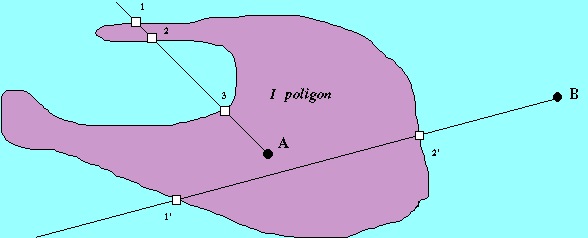
2.5 ábra - pont a poligonban algoritmus magyarázó ábrája

Tekintsük a 2.5 ábrát. Húzzunk az A pontból egy tetszőleges félegyenest. Határozzuk meg a metszéspontjait az I poligonnal. Az ábra tanúsága szerint három ilyen pont van. Ha az A-tól legtávolabbi metszésponttal kezdjük a pontok sorszámozását úgy a félegyenes végpontjának (A) a sorszáma 4 lesz. Végezzük el ugyanezeket a műveleteket a kívülálló B pontból is. A B pontra az előbbiek szerint adódó sorszám 3. Kísérletünket általánosítva megállapíthatjuk, hogy a pont akkor van a poligonban, ha a belőle húzott félegyenes poligonnal alkotott metszéspontjainak számát párosra egészíti ki, és akkor van az idomon kívül, ha a metszéspontok száma plusz egy - páratlan szám.

(A definícióba azért kell bevonni magát a pontot is, mivel külső pont esetén a félegyenes gyakran egyáltalán nem metszi az idomot, azaz 0 metszéspontja van a poligonnal. Mivel a 0 se nem páros se nem páratlan, ezekben az esetekben nem volna megoldás, ha a 0 összeghez nem adnánk hozzá magát a pontot is, azaz egyet).

Háló modell

A háló elmélet alkalmazásának gondolata az utóbbi néhány évben foglalkoztatja a grafikus adatok modellezésében érdekelt szakembereket.

Maga az elmélet az 50-es évek végétől jelentkezik összefoglaló monográfiákkal (lsd. pld. [1]). Az újabb matematikai irodalom mint a számítástudomány megalapozásának egyik modern algebrai területét tárgyalja a témát [2].

A háló elmélet a rendezési fogalomra épül. Maga a rendezés bennfoglalási és azonossági relációkat fogalmaz meg valamely halmaz elemei között.

Részlegesen rendezett halmazról akkor beszélünk, ha a bináris bennfoglalási relációval rendelkező P halmaz minden x, y, z elemére érvényesek az alábbi kijelentések:

(reflexivitás)

(1)

(antiszimetria)

(2)

(tranzitivitás)

(3).

Ha létezik az x y reláció, úgy x és y összehasonlíthatóak.

A térinformatika kérdéseire a területi beosztásokat illetően azonban a részlegesen rendezett halmazok segitségével nem minden kérdésünkre kapunk választ.

Képzeljük el, hogy egy területet (például egy országot) különböző szempontok szerint zónákra osztunk (pld. megyehatárok, vízügyi igazgatóságokhoz tartozó területek, környezetvédelmi felügyelőségek hatáskörzetei). Tegyük fel azt a kérdést, hogy melyik az a legnagyobb terület, melyet a régiók adott halmaza (pld. Pest megye, a Középdunavölgyi Vízügyi Igazgatóság területe, a Győri Környezetvédelmi Felügyelőség) magában foglal. Matematikai nyelven a legnagyobb alsó határt (infinumot) keressük. Sajnos azonban a részlegesen rendezett halmazok nem mindig rendelkeznek legnagyobb alsó illetve a vele duális legkisebb felső határral (suprémummal). Előző példánk esetében a legkisebb felső határ az a legkisebb terület, mely a kérdéses halmazelemeket tartalmazza.

A háló egy olyan parciálisan rendezett halmaz, melyben minden elempárra létezik supremum és infinum. Ha ez tetszés szerinti elem párra érvényes úgy teljes hálóról beszélünk. Minden részlegesen rendezett halmaz beágyazható egy teljes hálóba: ez a normál kiegészítő háló.

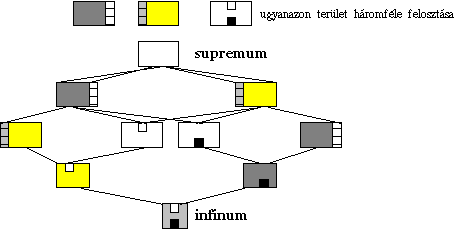
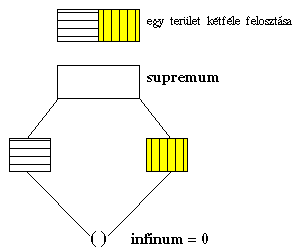
A részlegesen rendezett halmazok és hálóvá történő kiegészítésük kis elemszám esetén jól ábrázolható az un. HASSE-féle diagrammok segítségével. A 2.6 ábra egy bonyolultabb, a 2.7 ábra egy egyszerűbb területfelosztás HASSE-diagrammját ábrázolja. Ez utóbbi esetben az infinum üres halmazként adódik, mivel B-nek és C-nek nincs közös területe.

A háló modellben tárolt földrajzi információ lehetővé teszi a bennfoglalási (tartalmazási) kérdések egyszerűbb megválaszolását és a modell új eszközökkel (halmazműveletek) támogatja a fedvénymetszési (overlay) eljárások végrehajtását. A módszer a fejezet írásakor (96. 11.) még csak az elméleti megalapozás állapotában volt. Európában a modellel kapcsolatos kutatások W. KAINZ bécsi kartográfia professzor (jelenlegi munkahelye az ITC Entschede, Hollandia) nevéhez fűződnek (lsd. pld [3]).

2.6 ábra - egy terület háromféle felosztása, közös rész megtalálása
2.7 ábra - egy terület kétféle felosztása, melyeknek nincs közös része

ˇ        a következő részben megkezdjük a tesszellációs modellek ismertetését,

ˇ        visszatérhet az előző részhez is,

ˇ        vagy a tartalomjegyzékhez.

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc