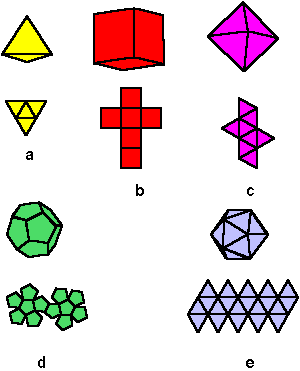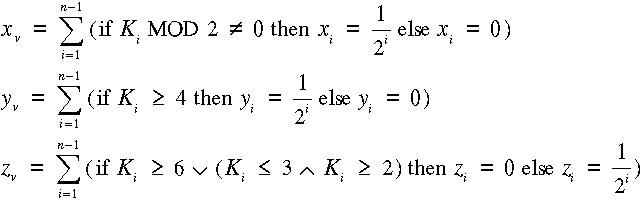Valódi térbeli (2.5 és 3 dimenziós) adatmodellek

P>Ebben a részben a valódi térbeli modelekkel foglalkozunk. Ezen belül megismerkedünk:

a 2.5 D-s modellezéssel,
a térbeli objektumok modellezési módszereivel éspedig,

a szabályos térbeli objektumok modellezésével,
a szabálytalan térbeli objektumok modellezésével,
a szabályos térbeli tesszellációval,
a szabálytalan térbeli tesszellációval.

Az utolsó évtizedben egyre nagyobb érdeklődés nyilvánul meg, elsősorban a föld- és bányászati tudományok részéről, Földünk belsejének háromdimenziós modellezésére. A témakör új voltát talán meggyőzően illusztrálja két évszám: 1985-ban Harrogate-ben a Nemzetközi Bányamérő Egyesület VI. Kongresszusa alkalmából rendezett kiállításon mutatta be az angol Szénhivatal első kísérleti 3 dimenziós bányászati tervezőrendszerét, s ugyanezen a kongresszuson két előadás szólt a 3D-s modellezés bányászati alkalmazásáról (M. Kavouras Kanadában tanuló görög doktoranduszé [13] és a szerzőé [14]); a második évszám 1989, ekkor mutatta be első kereskedelmi 3D-s modellező rendszerét az AUTO-CARTO 9 konferencián a Dynamic Graphics, Inc. kaliforniai cég [15].

A számítógépes három dimenziós modellezés más célú felhasználása sem tekinthet egy évtizednél hosszabb időre vissza. A 80-as évek első felében jelentek meg az első gépészeti 3 D-s CAD és CAM rendszerek, az évtized végére pedig az építészeti tervezésbe is bevonult a módszer.

A térinformatika kapcsolatrendszerében az alábbi három fő törekvési irány igyekszik hasznosítani a valódi térbeli modellezést:

a földtani és bányászati modellezés;
térhatású, az épületeket is megjelenítő elektronikus és nyomtatott térképek;
föld alatti és föld feletti skalár terek modellezése, elsősorban a környezetvédelem-környezetgazdálkodás szempontjai figyelembevételével.

A felsorolt három irányzat céljai eléréséhez különböző adatmodelleket használ. Ha a feladat valamilyen szabálytalan alakú térbeli tömb (pld egy telér) leírása, úgy a vektoros és tesszellációs modellek 3 D-s megfelelői kerülnek alkalmazásra. A szabályos elemi testekből álló objektumok esetén a vektoros vagy tesszellációs modell különleges válfajai a határleírás és a konstruktív test geometria felhasználása nyujtja a legjobb eredményeket. Vezérgörbével és állandó keresztmetszettel leirható objektumok modellezését legegyszerűbben pásztázással oldhatjuk meg. A litoszféra, hydroszféra és atmoszféra modellezése esetén rendszerint kevés adatból kell megbízható modellt alkotni, ezért ezekben a feladatokban különösen fontos szerepe van az interpolációnak. A cél sok esetben olyan térbeli attribútum tömbök levezetése melyek megjelenítése különböző értelmű és értékű izofelületekkel lehetséges. Az attribútum mezők jellege szabja meg az izofelületek milyenségét.

2.5 D-s modellezés

A digitális magasságmodell fogalmának bevezetésekor, tulajdonképpen már megismertük ezt a modellezési eljárást. Lényege, hogy a vizsgált térbeli felületet olyan síkkal helyettesíti, melynek minden pontjához attribútumként rendeli hozzá a magasságokat. Egyértelmű, hogy ezzel a módszerrel csak olyan felületek írhatók le, melyek magassága az alapsíkra vonatkozóan egyértékű fügvénnyel írható le. Bár elvileg lehetséges volna többértékűség esetén a felület alapsíkját megváltoztatni és olyan síkra vetíteni, melyre a többértékűség nem áll fenn, ez a módszer a gyakorlatban nem terjedt el.

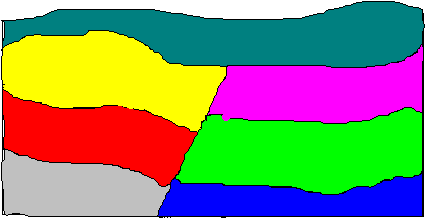
2.45 ábra - geológiai rétegek vetővel

E térképi adatok digitalizálásával nyerhetünk bemenő adatokat 2.5 D-s rétegmodellünkhöz. A rétegek mélységeit rendszerint négyzetháló sarokpontjaira interpoláljuk. A földtani viszonyok jobb visszaadása gyakran megköveteli, hogy modellünket sík vetőkkel egészítsük ki (2.45 ábra).

A 2.5 D-s modell továbbfejleszthető két felület által határolt rétegek reprezentálására is. Ezt a módszert elsősorban akkor célszerű alkalmazni, ha kis felbontású globális földtani modellt kivánunk létrehozni. E modelleket hagyományosan, mélységi illetve rétegvastagsági izovonalakkal ábrázolják, melyeket a geológusok mérési eredmények és szakmai szabályok alapján szerkesztenek.

Ha a bemenő adatok fúrásszelvények diszkrét pontjaiban adottak, úgy célszerűbb a mélységi információt ezekben a pontokban tárolni, s a felületekre jellemző kapcsolatokat e pontokra szerkeszthető, egyértelmű Delaunay háromszögeléssel reprezentálni.

A 2.5 D-s logikai adatmodell, az elmondottak értelmében a következőképpen foglalható össze:

réteg	felület	vető
<felső határoló felület> <alsó határoló felület> <attribútumok>	<pontok> <háromszögrács> <értelmezési tartomány> <attribútumok>	<síklapok> <elvetés mértéke> <attribútumok>

A közös határral rendelkező rétegek esetén a határt természetesen csak egyszer tároljuk. A felületet szórt pontjaival és háromszög hálózatával vagy levezetett négyzethálójával adjuk meg, a hozzájuk tartozó értelmezési tartományt pedig poligonokkal határoljuk le. A felsorolt logikai egységekhez tetszőleges számú attribútum rendelhető. Mivel a rétegek többféle szempont alapján alakíthatók ki, át is fedhetik egymást, sőt tartalmazhatják is egymást (gondoljunk a talajvízre, mely több réteget is tartalmazhat).

Már most érdemes rámutatni, hogy mind a réteg-, mind a testmodell az esetek jelentős részében számottevő elhanyagolásokat tartalmaz a valóságot hűebben leíró skalár- és vektortér modellezéssel szemben.

Térbeli objektumok modellezési módszerei

A térbeli objektumokat szabályos és szabálytalan objektum osztályokba sorolhatjuk. Az osztályozást gyakorlati szempontok indokolják.

Első szempontként az objektumra vonatkozó ismereteink eredetét említhetjük. A szabályos objektumok rendszerint aktuális vagy valamikori tervezés, és ez utóbbi esetben, ha megvalósult objektumokról van szó, emberi munka eredményei. Tervezett alakja és méretei ismertek, megvalósult alakja és méretei meghatározhatóak. A szabálytalan objektumok alakját és méreteit általában nem ismerjük pontosan, ezek közelítő meghatározása, viszonylag kis számú határoló pont ismeretében, különböző interpolációs eljárásokkal lehetséges.

Második szempontként megemlítjük, hogy szabályos objektumok esetén a modellezési módszerek viszonylag egyszerűbbek.

Végül indokolja az osztályozást a felhasználási terület is: a szabályos objektumokat elsősorban a gépészeti tervezésben, az építész- és mérnöki tervezésben, és kisebb mértékben, a bányászati tervezésben alkalmazzák, míg a szabálytalan modellek szinte egyeduralkodók a szélesen értelmezett földtudományok valamennyi területén.

Szabályos térbeli objektumok modellezése

Modellezés szempontjából legegyszerűbb szabályos objektumoknak a vonalas objektumokat tekinthetjük (kábelek, sinek, szállítószalagok stb.). Kezelésük és tárolásuk nem tér el lényegesen a már ismert síkbeli vonalas objektumokétól. Egyetlen különbség, hogy töréspontjaik kettő helyett három koordinátával vannak megadva, s ennek megfelelően a síkbeli egyenesekre megismert műveleteket egy dimenzióval bővíteni kell.

Az eltolási vagy forgatási szimmetriával rendelkező testek modellezésére egyszerű megoldást kinál a pásztázás (sweeping) módszere.

2.46 ábra - a pásztázás kétféle megvalósítása

Lényege, hogy egy terület (keresztmetszet) és egy pálya Descartes-i szorzata (x) reprezentálja a testet (2.46 ábra a fele). Bővíthető a módszerrel modelezhető testek tartománya kiegészítő műveletek alkalmazásával, bár az ilyen úgy nevezett hybrid modelleknél a számitástechnikai nehézségek viszonylag gyorsan növekednek.
A 2.46 ábra b felén egy ragasztásnak (K) nevezett halmazegyesítési eljárással kapcsoltunk össze két pásztázással modellezett elemi testet.

Keletkezésükkor a testábrázolás általánosabb módszerei is a többé kevésbé szabályos gépészeti formák modellezésére voltak orientálva. A módszerekkel szemben támasztott követelményeket a gépészeti CAD rendszerek követelményeiből kiindulva úgy fogalmazták meg, hogy az adott testek egyértelműek, konzisztensek legyenek és, hogy az adott leírás mind a számítási (pld. köbtartalom számítás), mind a rajzi igényeket kielégítse.

2.47 ábra - a határleírás módszer szemléltetése

Ez a kifejezés általánosítható, ha r az oldallapokon található üregek száma, h a testen áthaladó lukak száma, s pedig a testcsoport független elemeinek száma. Ebben az esetben:

v - e + f = 2(s - h) + r

.
Minden Euler képletet kielégítő test leírható öt operátorral és azok inverzével.

A határleírás igen előnyös a grafikus megjelenítés szempontjából, hátrányaként azt tartják számon hogy viszonylag nehezen módosítható az alakzat.

Az egyik leggyakrabban alkalmazott módszer a határleírás, tulajdonképpen a síkbeli vektoros modellek térbeli megfelelője. A módszer lényege, hogy a testeket határlapok uniójaként fogja fel, melyet kiegészít a határlapokat tartalmazó felületek definícióival. Magukat a határlapokat az élek unióinak tekinti (2.47 ábra).

A testek felépítése és lebontása elemi műveletekkel, az úgy nevezett Euler féle operátorokkal valósítható meg (lásd részletesebben pld. Mantyla és Sulonen tanulmányában [16]).

Ezek az operátorok nevüket a jól ismert Euler törvényekről kapták miszerint minden egyszerű poliaederben a lapok (f), élek (e) és csúcsok száma (v) között az alábbi egyenletben megfogalmazott szabály kell, hogy érvényesüljön:

v - e + f = 2

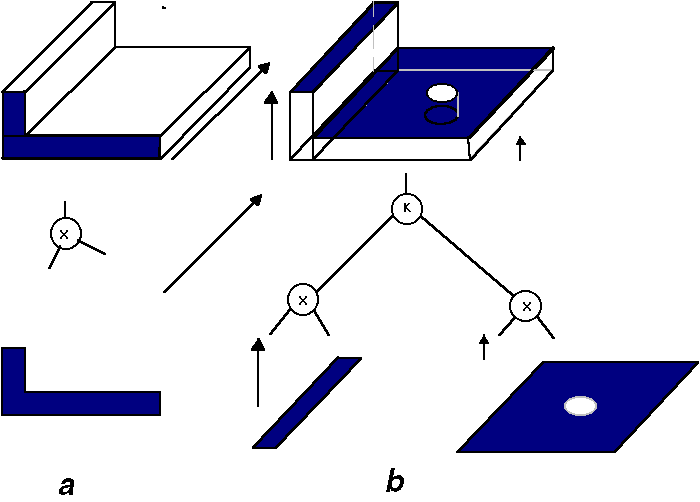
A konstruktív testgeometria alapgondolata a következő:

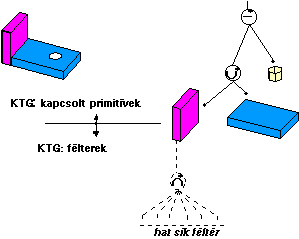
minden test felépíthető egyszerűbb testekből a regularizált Boolean műveletek az unió (), metszet (), összeg (), és különbség () segítségével.

Egyes modellekben primitív testeket: téglatesteket és hengereket alkalmaznak, más modellek alacsonyabb színtű primitív alkotóelemei a félterek. Ebben a megközelítésben egy blokk (téglatest) hat síkféltér regularizált metszése.

2.48 ábra - a konstruktív testgeometria módszer szemléltetése

A féltér azon E³-ban lévő P pontok együttese, amelyekre érvényes, hogy

{P: f(P)0},

ahol f=0 egy felület. Sík féltér alatt azokat a pontokat értjük, melyek az

ax + by + cz +d = 0

síkon és annak egyik oldalán helyezkednek el.

A konstruktív testgeometriai modellezés előnyös a módosítások és számítások szempontjából, közvetlen rajzi megjelenítése azonban nehézkes, ezért rajzi igények fellépésekor célszerű ezt a struktúrát előbb határleírásos alakba konvertálni.

Szabálytalan térbeli objektumok modellezése

A térbeli modellezés általános esetében a teret rendszerint elemi testek uniójaként fogják fel, azaz a térbeli tesszellációt alkalmazzák. Az objektumok megjelenítésekor pedig a tesszellációs modell alapján levezetik az ábrázolandó határfelületeket, azaz az ábrázolás közvetlen alapjául a vektor módszer térbeli megfelelője a határleírás szolgál.

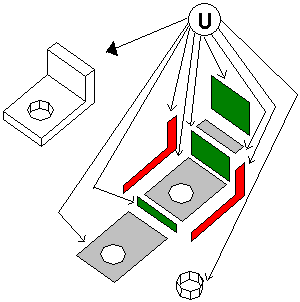
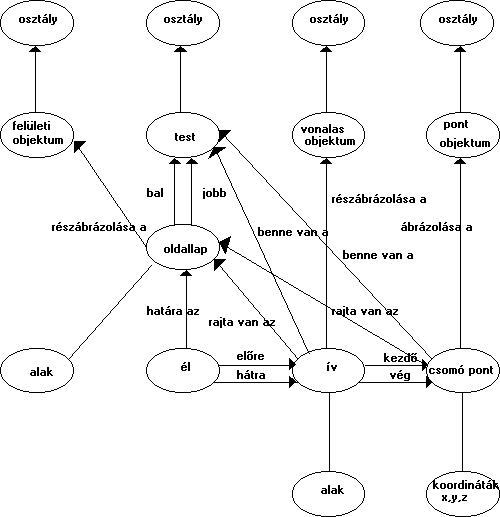
A térbeli földrajzi objektumok azonban nem csak testekből állnak, hanem a síkbeli vektoros adatmodellben már tárgyalt pontokból, vonalakból és területekből is. E megismert objektumok bővülnek a felületekkel illetve testekkel, melyek alkotóelemei az élekben találkozó határoló lapok. Ha ezenkívül még feltételezzük azt is, hogy valamely tulajdonságjellemzőjük azonossága alapján az egy objektum típushoz tartozó földrajzi objektumokat osztályokba is sorolhatjuk, ugy a vektoros 3D-s földrajzi adatmodell blokksémáját Molenaar nyomán [17] a 2.49 ábrában foglalhatjuk össze.

2.49 ábra - háromdimenziós topológiai adatmodell

A modellnek a tároláson, megjelenítésen és lekérdezésen kívül alkalmasnak kell lennie két objektum egymásra hatásának vizsgálatára is. E téma vizsgálata a közeljövő kutatási tematikáinak tárgyát fogja képezni. Annyi mindenesetre már ma is megállapítható, hogy a feladat viszonylagos egyszerűsítéséhez célravezetőnek látszik az objektumok tovább bontása primitív és összetett elemi objektumokra.

Nem igényel ugyanakkor nagy előrelátást annak a megállapítása, hogy az objektumok közötti műveletek a 2D-s vektoros modellekhez hasonlóan, de fokozott mértékben bonyolítják a raszteres modellben viszonylag egyszerűen elvégezhető metszési feladatokat. Nem téveszthetjük ugyanakkor szem elől, hogy a hierarchikus objektum struktúra a vektoros modell sajátja s ezért az objektum orientált lekérdezések és egyéb műveletek közvetlenül csak a vektoros adatmodellben realizálhatók. Valószínűsíthető, hogy a távolabbi jövőben a vegyes vektoros-tesszellációs modellek a 3D-s modellezésben is jelentősebb szerepet fognak játszani. Mivel azonban, amint már említtettük, a 3D-s modellezés még igen új szakterület, így módszerei fejlődésében és átértékelődésében már a közeljövő is szolgálhat néhány meglepetéssel.

A tesszellációs modelleket, síkbeli megfelelőikhöz hasonlóan, szabályos és szabálytalan osztályokba soroljuk.

Szabályos térbeli tesszelláció

2.50 ábra - szabályos testek

A szabályos modellek alapelemeit a szabályos síkidomokkal határolt öt úgy nevezett Plátón-i test a szabályos tetraéder (a), hexaéder (kocka) (b), oktaéder (c), dodekaéder (d) és ikozaéder (e) közül, választhatjuk, pontosabban a pentagon-dodekaéder nem elégíti ki a hierarchikus modell által megkívánt továbboszthatósági kritériumot, ezért figyelembe vételétől eltekinthetünk.

A globális földtudomány számára az ikozaéder modell tekinthető a legperspektívebbnek, mivel ez közelíti meg legjobban a gömböt, mely bizonyos célokra a Föld modelljeként is elfogadható.

A gyakorlati feladatok azonban általában korlátozott kiterjedésű helyi jelenségek modellezését igénylik, rendszerint a hasznosítható ásványok telepeinek leírására kerülnek felhasználásra. A szabályos modellek közül ilyen célokra, egyelőre, kizárólag a 2.50/b ábrán látható kockát alkalmazzák.

Ez a tény az egyszerűségen kívül elsősorban azzal magyarázható, hogy a kockák tömörítésére használt nyolcadolással létrehozható gráfok az úgy nevezett nyolcágú fák (octree-k) tárolására és manipulálására a négyágú fákra kidolgozott algoritmusok viszonylag egyszerű általánosítás után kiválóan alkalmazhatók (sok algoritmust, már eredetileg is n dimenzióra dolgoztak ki).

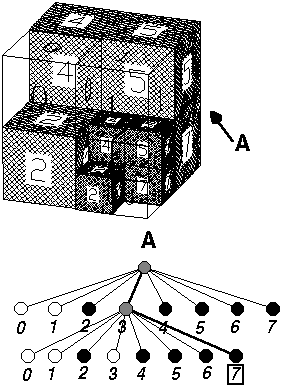
A 2.51 ábrán egy egyszerű térbeli objektum (A) kockákra bontását és az eredmény nyolcágú fáját mutatjuk be.

Természetesen az elemi kockák, idegen szóval voxelek, a képmátrixhoz hasonlóan, tömbökben is tárolhatók, kézenfekvő, hogy e tömbök dimenziója bináris objektumok esetén három. A tömbös (más szóval direkt vagy bithalmazos tárolás) előnyös a halmazműveletek közvetlen végrehajthatósága szempontjából, ugyanakkor nagy hátránya a jelentős tárolási igény.

Sajnos a hagyományosan alkalmazott pointeres octree-s tárolásnál, amikor a fa ágait mutatókkal láncoljuk egymáshoz (a keresési algoritmusok meggyorsítása érdekében általában két irányban), az elkerülhetetlen 32 bites mutatók miatt nem várható drasztikus csökkenés a tároló helyekben.

2.51 ábra - nyolcágú fa felbontás

Legjobb megoldásnak pillanatnyilag a lineáris octree tűnik, mely csak a levél szinten lévő fekete voxeleket tárolja a helyzetüket és nagyságukat leíró iránykóddal. Az iránykód egy olyan karaktersorozat, melynek elemeit, a gyökértől kezdődően, a hierarchia szint növekvő sorrendjében, a kérdéses fekete levélhez vezető ágak iránykódjai alkotnak. Az iránykód hossza megadja, hogy a voxel hányadik hierarchia szinten található, azaz hogy milyen nagy. Ha a gyökér szintnek (0. hierarchia színt) megfelelő befoglaló kocka térfogatát egységnyinek tekintjük, úgy az i-ik hierarchia szinten található voxel köbtartalma

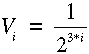
A 2.51 ábra jelölt voxele (második hierarchia színt, 7. levél) például lineáris octreevel a következőképpen írható le: 37, köbtartalma pedig a bemutatott képlet felhasználásával: 1/64.

Ha az X, Y, Z térbeli derékszögű koordinátarendszer O kezdőpontját az A befoglaló kocka hozzánk közelebb fekvő bal alsó sarkába helyezzük el, úgy az egyes levelek által reprezentált voxelek analóg (hozánk közelebb fekvő bal alsó) sarokpontjainak koordinátáit a táblázat baloldalán látható kifejezésekből számíthatjuk. K_i az i.-ik hierarchia színt iránykódját jelenti.

Már utaltunk rá, hogy a voxeles adatmodell népszerűségét viszonylagos egyszerűségén kívül elsősorban az magyarázza, hogy a raszteres (pixeles) kétdimenziós modellnél kidolgozott algoritmusok a harmadik dimenzió bevezetésével könnyen általánosíthatók a voxeles modellra. Az előző fejezetben ismertetett fogalmakat, algoritmusokat illetve módszereket most nem kívánjuk kibővítve újra tárgyalni, csak utalunk néhány szempontra, melyet a bővítésnél célszerű figyelembe venni.

A legegyszerűbb a távolság fogalmak kiterjesztése. Valamennyi képletre igaz az a szabály, hogy háromdimenziós esetben kibővítendők a z koordináták különbségeivel is, mégpedig ugyanolyan formában, ahogy az adott kifejezés a másik két koordináta különbséget tartalmazza.

Nem jelent elvi problémát a halmazműveletek és a területszámítás általánosítása (azaz a köbtartalom számítás) sem. Bithalmazos (tömbös) tárolás esetén az unió vagy metszet ciklusmagja ugyanaz mint kétdimenziós esetben, csak a környezete változik annyiban, hogy a kérdéses ciklust a háromdimenziós tömbök mind a három ciklusváltozója szerint lefuttatjuk. Ugyanez a helyzet a köbtartalom számításnál is azzal a különbséggel, hogy a műveletben csak egy háromdimenziós tömb vesz részt és a három ciklus ennek a fekete voxeljeit számolja össze.

Octree-s tárolásnál az elmondottak minden változtatás nélkül alkalmazhatóak a 3D-s halmazműveletekre is csak azt kell figyelembe venni, hogy az összehasonlítást hierarchia szintenként nem 4 hanem 8 csomópontra kell elvégezni. A köbtartalom számítás lineáris octree tárolás esetén szintén nem okozhat különösebb gondot. Olyan programot kell összeállítanunk, mely megszámolja az egyes ágakban lévő iránykódok számát és feltölt velük egy egydimenziós tömböt. A tömb mérete megegyezik a tárolt fekete voxelek számával. Magát a köbtartalom számítást egy olyan ciklus végzi, mely sorra behívja a tömb elemeit, a köbtartalom képlettel kiszámolja a kérdéses voxel köbtartalmát és hozzáadja az előző voxelek köbtartalom összegéhez. A végösszeget akkor kapjuk meg, ha a ciklus annyiszor futott le ahány fekete voxelt tároltunk.

Kissé bonyolultabb az általánosítás a kerület illetve az annak háromdimenziós esetben megfelelő felület esetében. A problémát tulajdonképpen az jelenti, hogy háromdimenziós esetben a szomszédsági osztályok is bővülnek és ennek megfelelően újabb felület fogalmakat is bevezethetünk. Míg a kétdimenziós esetben a d-szomszédság (a pixelek oldalaik mentén találkoznak) és az i-szomszédság (a pixelek sarkai találkoznak), tehát két szomszédság fogalom három kerület fogalom meghatározását tette lehetővé, addig a voxelek esetében három féle szomszédságról is beszélhetünk (a voxelek lapok mentén találkoznak - a d-szomszédság megfelelője, élekben találkoznak - i-szomszédság, csúcsukban találkoznak - új fogalom, nevezzük c-szomszédságnak), következésképpen lehetőségünk van bővíteni a határoló felület fogalmát is. A gyakorlat számára azonban továbbra is a d-szomszédságon alapuló felület fogalmat célszerű alkalmazni, ekkor viszont az ismertetett kerület meghatározó algoritmus 3D-s általánosításával érhetünk célt. Végül megjegyezzük, hogy Samet már többször idézett munkájában [4] a legtöbb algoritmust már eleve n dimenzióra kiterjesztve találjuk.

Szabálytalan térbeli tesszelláció

A háromdimenziós modellezést rendszerint földalatti objektumok pld. érctelérek, széntelepek modellezésére használják. A rendelkezésre álló információ gyakran hiányos, a rendszerint szabályos rácsban elhelyezkedő fúrásszelvények nem feltétlenül az objektumot határoló felület jellemző töréspontjairól nyújtanak információt. Ilyen körülmények között indokolt a szabályos tesszelláció az előző pontban ismertetett voxeles modell alkalmazása, mivel szabályos elrendezésének köszönhetően viszonylag egyszerű számítási és megjelenítési algoritmusokkal rendelkezik. Az is igaz, hogy a felbontás növelésével a voxeles modell elvileg képes a pontos információkat is a megkívánt finomsággal visszaadni. A probléma csak az, hogy ezekben az esetekben a voxeles modell bizonyos feladatokra nem éppen a leggazdaságosabb.

Ez a tény vezetett a szabálytalan tesszellációs modellek kialakulásához. A szabálytalan tesszellációban elemi testeként a napjainkig ismert módszerek a szabálytalan tetraedert alkalmazzák. Ha ismerjük az objektum n db. x,y,z koordinátával jellemzett pontját, úgy e pontokra az egyértelmű és bizonyos, később ismertetett szempontok szerint optimális tetraeder felbontás elvégezhető, ha megelégszünk a pontokat burkoló konvex héjjal.

Ne felejtsük el, hogy a vázolt feladatban valamennyi ismert pont attribútuma azonos, s csak azt fejezi ki, hogy a kérdéses pont az objektumhoz tartozik. Ha a pontok attributum értékei a tér valamely változó tulajdonságú jellemzőjét (pld. hőmérséklet, kénkoncentráció, porozitás stb.) írják le, úgy az optimális háromszög illetve tetraeder felbontás a 2D-s és 3D-s skalártér modellezés eszköze.

Határesetként vehetjük figyelembe a mérnöki gyakorlatnak azt a Magyarországon különösen aktuális feladatát, amikor a város alatt húzódó alagút (pince) labirintus 3D-s modellezésére van szükség. Ha az alagutak felmérését geodéziai-bányamérési módszerekkel végezzük, úgy minden pontról tudni fogjuk nem csak azt, hogy az objektumhoz (alagúthoz) tartozik, hanem azt is, hogy az alagút határoló felületén helyezkedik el. Ez a plusz információ, amint azt az alábbiakban látni fogjuk, lehetővé teszi, hogy az egyértelmű tetraéder felbontást tetszőleges alakú, tehát nem csak konvex, objektum esetén elvégezhessük.

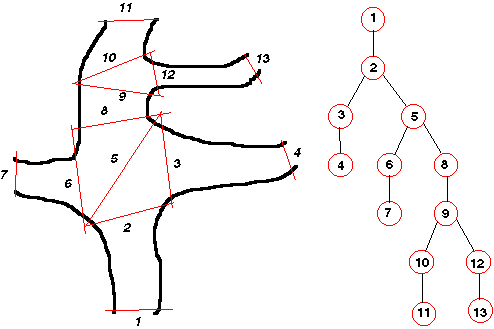
Kvázi keresztszelvényekkel bemért alagút digitális modellje.

Amint az a módszer elnevezéséből is kitűnik, alkalmazhatóságának feltétele, a felmérést keresztszelvények segítségével hajtsuk végre. Azért beszélünk kvázi keresztszelvényekről, mivel az eljárás nem igényli, hogy a szelvények síkok legyenek, csak azt, hogy a szelvények ne messék egymást.

Az oldalágak fellépését kettéágaztatással vesszük figyelembe, ami azt jelenti, hogy mind a felmérésnél, mind a feldolgozásnál egy alagút szakasznak csak két követője lehet. A 2.52 ábra jól szemlélteti az elmondottakat: az 1 és 2 keresztszelvények közötti egyenes szakasz után három irányba is elágazik a barlang, de mivel a modellünk csak kettős elágazásokat kezel, a hármas elágazást két egymás után következő kettős elágazásra bontjuk.

2.52 ábra - kvázi keresztszelvények elágazó alagútban

A 2 szelvénytől kezdődően az elágazás először a 3 és 5 szelvényekkel indul, majd az 5 szelvényből kiindulóan a 6 és 8 szelvények felé. Kézenfekvő, hogy ez a megoldás csak akkor alkalmazható, ha az 5 szelvényt a helyszínen is kitűztük és bemértük.

2.53 ábra - a felület háromszögelése két keresztszelvény között (elágazás nélküli szakasz)

Meghatározzuk mindkét keresztszelvény súlypontját és a két súlypontot összeillesztve egymásra helyezzük a súlypontokat összekötő tengelyre merőleges síkra vetített keresztszelvényeket (ne felejtsük, hogy a felmérés során nem kötöttük ki a keresztszelvények sík voltát, mivel ez jelentősen nehezítette volna a terepi munkát, csak azt a követelményt támasztottuk, hogy a kvázi-keresztszelvények nem metszhetik egymást). Az összevetítés eredményeképpen, kedvező esetben, az egyik keresztszelvény magában foglalja a másikat. Mivel algoritmusunk erre a feltételezésre épült, abban az esetben ha a keresztszelvények metszik egymást olyan mértékben változtatjuk meg az egyik keresztszelvény méretarányát, hogy a bennfoglalási követelmény kielégüljön.

A palástot reprezentáló háromszöghálózat szerkesztését a két keresztszelvény egymáshoz legközelebb eső két pontjának összekötésével kezdjük (2.53 ábra). A következő háromszögoldal meghúzására két lehetőségünk is van (ha egy haladási értelmet pld. az óramutató járásával megegyezőt előírunk): ugyanis az első oldal első vagy második végpontjából is indulhat a következő háromszögoldal. Azt az oldalt választjuk a két lehetséges közül, mely kisebb szöget zár be a súlypontból az oldal felezőjébe húzott egyenessel. Az eljárást az elmondottak szerint mindaddig folytatjuk, amíg a két keresztszelvény között a háromszöghálózat teljes nem lesz.

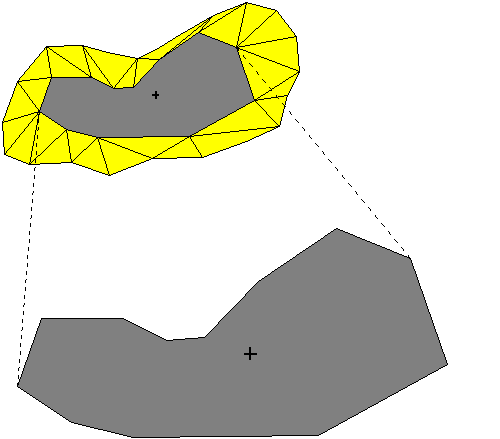
Két keresztszelvény között a barlang határfelületét háromszöghálózattal modellezzük, azaz tulajdonképpen a határleírás módszerét használjuk. Ha erről a modellről szabálytalan tesszellációra azaz tetraéderes felbontásra akarunk áttérni, úgy magukon a síkba vetített keresztszelvényeken is el kell végezni a háromszögfelbontást. Ezután sorra véve valamelyik keresztszelvény háromszögeit és a hozzájuk csatlakozó háromszögeket a paláston megkapjuk a szakaszt alkotó tetraéderek első részét, az eljárást a másik keresztszelvénnyel megismételve pedig a másikat. Térjünk azonban vissza a palást modellezésére.

Az elágazások helyein a két ághoz is tartozó (nagy) keresztszelvényeket már a felmérés során két részre kell bontani (be kell mérni az elválasztó vonal két pontját), majd a háromszög hálózatok megszerkesztését a két rész számára a korábban elmondott módon végezzük azzal a különbséggel, hogy a közös keresztszelvény egy-egy felét úgy tekintjük mintha olyan önálló keresztszelvény volna, melynek két pontja azonos egy másik keresztszelvénnyel.

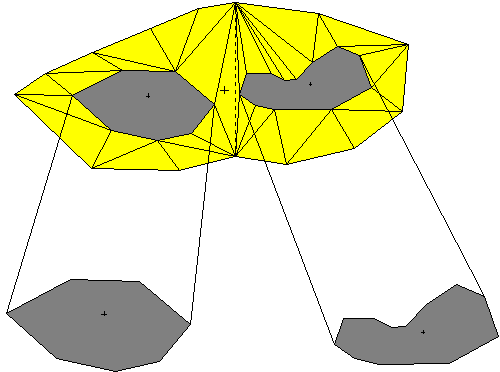
2.54 ábra - a felület háromszögelése elágazó szakaszon

Az elmondottakból következik, hogy a két részkeresztszelvényt a hozzájuk tartozó ág másik végének keresztszelvényével együtt a saját ághoz tartozó súlypontokat összekötő egyenesre merőleges síkra vetítjük, ami természetszerűen különböző a két ágra (2.54 ábra).

A szabálytalan tesszelláció általános esete szoros kapcsolatban áll a Delaunay háromszögeléssel és duálisával a Voronoi tesszellációval. Mivel ez a módszer különösen jelentős szerepet játszik a térinformatikában számos területén, tárgyalásának egy külön pontot szentelünk.