Fotogrammetriai módszerek a pontok helyzetének meghatározására II

Ebben a részben megismerkedünk

a fotogrammetriai termékekkel és módszerekkel , ezen belül

a koordináták és koordináta együttesek meghatározásával,
a vektoros térképkészítéssel és
a tónusos termékekkel és előállításukkal;

illetve a digitális fotogrammetria univerzális feldolgozó eszközével a

fotogrammetriai munkaállomásokkal.

Termékek és módszerek

A digitális fotogrammetria főtermékei:

koordináták és koordináta együttesek;
vektoros térképek;
tónusos térképek

digitális formában. Természetesen megfelelő perifériák segítségével ezekből az állományokból nyomtatott illetve rajzolt termékeket (hardcopy) is elő lehet állítani.

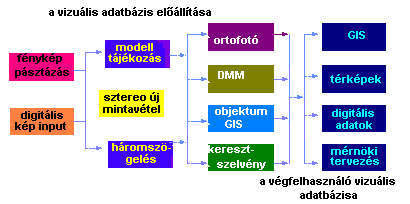
A digitális fotogrammetria munkafolyamatát jól szemlélteti a 3.45 ábra.

3.45 ábra - a digitális fotogrammetria munkafolyamata

Az ábra bal oldala azokat a műveleteket foglalja össze, melyeket a fotogramméterek végeznek a virtuális adatbázis létrehozása érdekében.
A bemenő adatok, amint azt az előző részben már részleteztük, vagy eleve digitális fényképezés eredményei, vagy az analóg felvételek szkennelésével jönnek létre.

A következő lépésben sor kerül a modell tájékozására, a fotogrammetriai alappont meghatározásra, illetve szükség esetén a képminőség javítására (erről egy következő részben szólunk).
A jelenlegi fejezet tárgya tulajdonképpen a következő négy blokk: az ortofotó készítés, a Digitális Magasság Modell előállítás, a vonalas (objektum) kiértékelés és a keresztszelvény készítés, mely utóbbi elsősorban nem a GIS, hanem a mérnöki tervezés szempontjából fontos, ezért erre a témára nem térünk ki.
Az utolsó négy blokk arra utal, hogy ugyanazok az adatok különböző feldolgozottsági szinten illetve különböző rendezésben mint virtuális adatbázisok jelentkeznek a különböző szakmájú végfelhasználók számára.

A kordináták és koordináta együttesek meghatározása

A földi pontok koordinátáinak ismerete szükséges a külső tájékozási adatoknak a kollinearitási feltételeken alapuló meghatározásához. A fotogrammetriai módszerek gazdaságosságát igyekeztek azzal fokozni, hogy a képenként szükséges négy illesztőpontot részben fotogrammetriai módszerrel határozták meg. Ha ugyanis az első kép tájékozási adatai földi pontok felhasználásával meghatározhatók úgy felírhatjuk a kollinearitási egyenletek sorba fejtett variánsait olyan pontokra is melyek két vagy három egymást követő képen megtalálhatók. A sor meghatározott részein ismert koordinátájú földi pontokat is találunk, melyekre az egyenleteket ismét felírjuk. A túlhatározott rendszert kiegyenlítéssel kiszámolva, megkapjuk a képeken kiválasztott pontok földi koordinátáit. E pontok segítségével valamennyi kép külső tájékozási adatát kiszámolhatjuk és a további feldolgozásban felhasználhatjuk. A röviden vázolt módszert sugárnyaláb kiegyenlítésnek hívják.

Bonyolult terepi körülmények között (pld. sivatagban) célszerű lehet az illesztőpontokat nem csak előre jelölni de állandósítani is és koordinátáikat az esetleges kitűzési munkák során felhasználni. A térinformatikai adatnyerés szempontjából azonban maguk a légi háromszögeléssel nyert koordináták (ellentétben a külső adatokkal) nem bírnak nagy jelentőséggel. Talán a leglényegesebb terméke a digitális fotogrammetriának ugyanakkor, a rendezett koordináta együttesként is felfogható digitális magasságmodell vagy angol rövidítéssel DEM . Amint arról már szóltunk, a modellt létrehozhatjuk jól kiválasztott szórt pontokra támaszkodva is, ezt a modellt nevezik TIN-nek. A TIN létrehozása azonban egyelőre még nem automatizálható és aktívan igényli a földi felmérő vagy fotogrammetriai kiértékelő közreműködését. A DEM azonban az első olyan termék, mely létrehozását automatizálták, ezért egy kissé bővebben vázoljuk fel a folyamatot.

A DEM szabályos rácsban (pld 50 m. x 50 m.) tárolja a magasságokat. Létrehozható földi mérési módszerekkel , fotogrammetriai módszerekkel, sőt a későbbiekben tárgyalandó GPS módszerekkel is. Ha a kisebb részletektől eltekintünk, úgy azt mondhatjuk, hogy mindhárom mérési módszer esetén két fő stratégiát alkalmazhatunk a DEM létrehozására: vagy közvetlenül a szabályos rácspontokban mérjük a magasságokat vagy többé-kevésbé rendszertelenül elhelyezkedő pontokban mérünk, és a kapott értékekből interpolációval vezetjük le a szabályos magassági rácsot. A digitális fotogrammetriai adatnyerés esetén még azt is megválaszthatjuk bármely stratégia szerint is kívánunk eljárni, hogy emberi közreműködéssel vagy a nélkül kívánjuk elvégezni a mérést.

A digitális fotogrammetriai kiértékelést a fotogrammetriai munkaállomás segítségével hajtjuk végre.

Ha emberi közreműködéssel végezzük a kiértékelést, úgy a már korábban meghatározott külső tájékozási adatok felhasználásával (vagy illesztőpontok segítségével) tájékozzuk a képpárt, beállítjuk a rácsoldalak hosszát és beindítjuk az eljárást. A számítógép ezután XY értelemben az első rácspontba vezérli a mérőjelet az operátor pedig a sztereoszkópikus látás felhasználásával egy tárcsa segítségével rávezeti a mérőjelet a terepre és egy gomb megnyomásával nyugtázza a művelet elvégzését. A mérőjel ezután a következő pontra áll és a művelet mindaddig folytatódik míg a tartomány utolsó rácspontja nem kerül sorra. Ezután a gép beállítja a következő modellt és a művelet folytatódik.

A második stratégia alkalmazása magasabb követelményeket támaszt a kiértékelővel szemben, a minőségi munka előnyei ugyanakkor szoftvertől függően többé vagy kevésbé elvesznek az interpoláló eljárás során. Ezért napjainkban ezt a módszert elsősorban TIN modellek létrehozására használják. Az operátor a terep sztereoszkópikus szemlélése alapján kiválasztja a terep jellemző pontjait és a mérőjel terepre illesztésével meghatározza azok mindhárom rendezőjét. A feladat megoldásához az operátornak már mindkét kezére szüksége van: egyik kezével a pozicionáló gömb (népszerű nevén "hanyat egér") segítségével vízszintes értelemben mozgatja a mérőjelet, másik kezével tárcsát mozgat, mely a mérőjel függőleges mozgását vezérli.

Az automatikus kiértékelési eset vizsgálatakor lapozzunk vissza a 3.40 ábrához. Ha a szabályos rácspontokat a normál-szterogramm baloldali képén definiáljuk (például 30 mm-es pixel méret, 1:10000 közelítő képméretarány, 60%-os átfedés, 30 m. x 30 m.- rács esetén kijelöljük, hogy a mérések y szerint a 3700-ik, 3600.-ik, 3500.-ik stb sorok x szerinti -800.-ik, -700.-ik, -600.-ik stb. pixeleire vonatkozzanak), úgy a kapott vízszintes modellkoordináták az (X), (Y), (Z) modellkoordináta rendszerben meg fognak felelni az elvárásoknak ( feltéve, hogy és b értékét helyesen adtuk meg), ha azonban az (X), (Y), (Z) koordinátákat áttranszformáljuk a vetületi koordináta rendszerbe úgy a rács nem lesz ÉK tájolású, kissé el fog térni a derékszögtől és a 30-m.-es lukbőségtől. Felfoghatnánk a kapott eredményt mint TIN struktúrát is mivel azonban a közel rács jellegű pontok számára igen előnytelen a TIN struktúra célszerűbb egy második lépésben a kvázi rácspontokat egy szabályos tájolású és lukbőségű rácsba interpolálni.

A rácspontok magasságát közvetlenül meghatározó módszer alkalmazása esetén először elvégezzük a normál-sztereogramm X,Y,Z koordináta rendszerének tájékozását a földhöz kapcsolt koordináta rendszerhez képest. A tájékozáshoz hét adatra (O₁ három koordinátájára, a tengelyek három elfordulás komponensére és a méretarány tényezőre) van szükségünk. Az adatok meghatározhatók, ha legalább két a képeken látható földi alappont vízszíntes és három alappont magassági koordinátáit ismerjük.

Megtervezzük a rács sarokpontok koordinátáit a földi rendszerben, majd a koordináta transzformáció kifejezésében a képkoordináták helyett a modellkoordinátákat szerepeltetve és kifejezve, a földi koordinátákat pedig görög nagybetűvel jelölve, a rács sarokpontok modellkoordinátáit a következő alakban írhatjuk fel:

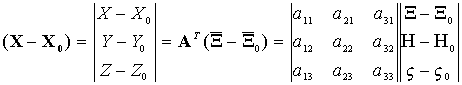illetve kifejezve a keresett értékeket:

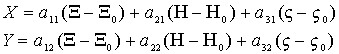A kifejezések jobb oldalán mindent ismerünk a magasság kivételével. Mivel azonban közel állótengelyű felvételeknél a₃₁ és a₃₂ közel zérus, míg a többi együttható értéke állótengelyű felvételeknél is párosával a 0 és 1 között változik a függvényében, első közelítésként eltekinthetünk a rácspontok modellkoordinátáinak számításánál a harmadik tagtól.

A rácspontoknak megfelelő x', y' baloldali képkoordináta értékek számításához a normál-sztereógramm kifejezéseiből kell kiindulnunk (ne felejtsük el, hogy a normál-sztereógrammban y'=y'' tehát ennek meghatározásával nem lesz több gondunk). Fejezzük ki a keresett ismeretleneket:

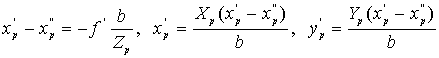A kapott kifejezésekből világos hogy az ismeretlenek száma nagyobb az egyenletek számánál, a megoldást tehát iterációs formában kell keresnünk.

Vegyünk fel Z értékeket (a terepről szerzett ismereteinket felhasználva), számoljuk ki az ennek a felvételnek megfelelő képkoordinátákat és az előző pontban ismertetett korrelációs elárással határozzuk meg a parallaxist. Ha a felvett érték és a számított érték megegyezik, akkor készen vagyunk, ha nem úgy újabb magasság felvételével folytatjuk a keresést. Mivel a felvett magasság az y' koordinátákat is befolyásolja, célszerű a magaságokat úgy lépcsőzni, hogy azok egy-egy pixelnyi ugrást eredményezzenek a sorok között.

A másik lehetőség a feladat megoldására kétdimenziós korrelációt igényel. ebben az esetben kis négyzeteket illesztünk különböző felvett magasság értékkel a rácspont köré. A normál-sztereógramm fenti kifejezéséből kiszámolhatjuk az adott magasságú ablak sarokpontjainak képkoordinátáit mindkét képen. Kiszámoljuk a különböző magasságú kép párokra a kétdimenziós korrelációt mindkét képen és az a magasság lesz a valódi, melyhez tartozó korreláció érték maximális. Ez a feladat nem normalizált tájékozott kép párokkal is megoldható, ebben az esetben azonban a normál-sztereógramm helyett az általános kifejezéssel kell az ablakok sarokpontjainak képkoordinátáit meghatározni.

Vonalas (vektoros) digitális térképek létrehozása.

Vonalas térképeket a digitális fotogrammetriában két módszerrel hozhatunk létre. Ipari körülmények között mindkét módszer operátori munkát igényel, azaz a kiértékelést programok támogatásával szakember végzi. Elvileg lehetséges e módszerek néhány főbb műveletének automatizálása is, e módszerek azonban egyelőre még csak kísérleti stádiumban vannak és a gyakorlatban elsősorban katonai feladatoknál kerülnek alkalmazásra.

A digitális fotogrammetriai munkaállomáson végrehajtott vonalas kiértékelés az operátor szempontjából nagyon hasonlít arra a munkára, amit a kiértékelő az analóg fotogrammetriai kiértékelő berendezéseken végez.

A feladat a sztereomodell tájékozásával kezdődik. A tájékozott modellt megjelenítő képernyőt az operátor szemüvegén keresztül a térben látja. Mivel a cél a terep síkrajzának kiértékelése, az operátor a pozicionáló gömb és egy kézi tárcsa segítségével ráhelyezi a térben lebegő mérőjelet a kiértékelendő vonalra (útra, patakra stb.) és úgy vezeti végig rajta, hogy az objektum felszínével érintkezésben maradjon. A kiértékelt pontok közül, az utasítás paraméterezésének megfelelően, a számítógép megadott út-, vagy idő intervallumonként rögzít egyet-egyet, illetve arra is van lehetőség, hogy az operátor gombnyomással jelezze a rögzítendő pontokat. A kiértékelő szempontjából lényeges különbség az analóg és digitális kiértékelés között abban jelentkezik, hogy a kiértékelt szakasz érzékelhető a képernyőn (pld villog) és utasításra regularizált képével helyettesíthető. Ez utóbbi azt jelenti például, hogy a kiértékelt szabálytalan vonalra a gép spline-t illeszt, vagy a nem derékszögűnek adódó házakat ortogonalizálja stb. Ha a kiértékelés célja hardcopy, úgy lehetőség van az egyezményes jelek (szimbólumok) beiktatására is. Mivel azonban általában a kiértékelés eredménye térinformatikai hasznosításra kerül (még akkor is ha a végcél papír térkép) a kiértékelés folyamatában az operátor létrehozza a kiértékelt vektorok topológiáját is.

Míg a hagyományos analóg vonalas kiértékelés a síkrajzon kívül kiterjedt a szintvonalak kiértékelésére is, a digitális fotogrammetriai munkaállomáson erre nincs szükség, mivel a magasságokat DTM-ben tárolják, s ha a papír térképen esetleg színtvonalakra volna szükség, úgy azok számítógépes programok segítségével a DTM-ből automatikusan levezethetők. A másik lehetőség vektorizált síkrajzi állományok létrehozására az ortofotó térképek digitalizálása. Ennek a módszernek az a nagy előnye, hogy nem igényel nagyon költséges fotogrammetriai munkaállomást, hanem megfelelő szoftver (pld INTERGRAPH MGE) felhasználásával megfelelően konfigurált PC-n is végrehajtható ( maguknak az ortofotóknak a létrehozása természetesen igényli a nagyteljesítményű számítógépet, de sokkal gazdaságosabb ezekkel a gépekkel csak azokat a feladatokat megoldani, melyek kisebb gépeken nem végezhetők s jelentős mértékben automatizáltak). Ha a digitalizálást mégis fotogrammetriai munkaállomáson hajtjuk végre, úgy a művelet az INTERGRAPH MSFC program modul teremtette környezetben végezhető.

A módszer lényege, hogy a digitális ortofotót behívjuk a futó programrendszerbe, és megfelelő ablakolás után a képernyőn ráállunk az egérrel vagy cursoral vezérelt szálkereszttel a digitalizálandó pontra. Cursor használata esetén itt is alkalmazható a folyamatos rögzítés valamelyik variánsa, a gyakorlatban azonban, tekintettel a gépek korlátozott kapacitására, rendszerint pontonkénti regisztrálást alkalmaznak. A további lépések főbb vonásaikban megegyeznek az előző módszerrel kapcsolatban elmondottakkal.

A folyamat részleges automatizálása mind tájékozott kép pár, mind ortofotó felhasználásával megoldható. Mindkét esetben azonban arra van szükség, hogy a későbbiekben ismertetendő képfeldolgozó eljárások felhasználásával élkiemelést és szűrést hajtsunk végre a kép páron illetve az ortofotón.

Ha kép párokat használunk úgy a baloldali képen létrejött összefüggő élekből mintaállományokat képezünk és kétdimenziós korrelációval megvizsgáltatjuk, hogy melyek az összetartozó élek. A keresési állományok kijelölése igen bonyolult feladat ezért részleteivel nem foglalkozunk, csak megjegyezzük, hogy a folyamat előrehaladásával élről élre a keresési állomány szűkíthető.

Ha ismerjük egy-egy él összetartozó koordinátáit a két képen ugy a megfelelő földi koordináták számíthatók. Ezután kerülhet sor az élet meghatározó pontok alaktól függő ritkítására, majd a generalizálásra és regularizálásra.

Ortofotó alkalmazása esetén nincs szükségünk a korreláció számítására, hisz a kiemelt élek már földi koordináta rendszerben vannak megadva. Ha az élkiemelés után olyan átkódolást alkalmazunk, hogy csak az élek legyenek feketék a többi terület pedig fehér, úgy a vektorizálási folyamatot az ismertetett módon hajthatjuk végre.

Az automatikus módszerek fő problémája, hogy a megvilágítási viszonyok helyi változásai (szaggatott felhőzet) valamint fedő objektumok (fák) véletlen megjelenése következtében a kiemelt élek szürkesége nem lesz egyenletes a két képen, és szakadások állhatnak elő a természetben folyamatos vonalban. A kutatók e problémákra igyekeznek megoldásokat találni egyre nagyobb sikerrel. Amíg azonban ez a siker nem teljes az automatikus módszerek csak akkor használhatók, ha a képernyőn operátori közreműködéssel javítjuk a módszer nyújtotta eredményeket, összehasonlítva a kapott vektorokat a térmodellel illetve az ortofotóval.

Tónusos térképek (ortofotótérképek)

Amint azt az előző részben vázoltuk egy tájékozott kép felhasználásával csak akkor állítható elő az objektum torzítatlan képe, ha az eredetileg sík volt. Ezt a tényt használták ki az analóg fotogrammetria egyképes eljárásai arra, hogy optikai-mechanikai vetítőberendezésekkel előállítsák a síknak tekinthető terepfelszín torzítás mentes fototérképét. Ha a terep a repülési magassághoz képest figyelemre méltó domborzattal rendelkezett a számítógépek felhasználása nélkül nem lehetett torzítatlan képeket előállítani a terepről.

Az első ortofototérképeket féldigitális technikával állították elő, mivel a végterméket egy igen bonyolult, számítógép vezérelt optikai-mechanikai berendezés fényképészeti módszerrel készítette.

A digitális fotogrammetria első nagy sikere a digitális ortofotótérképek tömeges előállításához kapcsolódik.

Az automatikusan előállítható ortofotó térképek ugyanis szinte minden olyan feladatra alkalmasak mint a hagyományos vonalas térképek, e mellett azonban az információ tartalmuk jelentésen meghaladhatja azokét, ugyanakkor gyorsan és olcsón állíthatók elő.

A módszert a normalizálással kapcsolatban felvázolt 3.41 ábra segítségével érthetjük meg. Tekintsük a baloldali pixeleket az ortofotó földi X,Y,Z koordináta rendszerének X,Y síkjában fekvőnek és számítsuk ki az egyes földi pixelközéppontoknak megfelelő helyeket a rajz jobboldalán ábrázolt fényképen. Ahhoz, hogy ezt meg tudjuk tenni szükségünk van a pixelközéppontok Z koordinátáira is, ezért az ortofotó térkép készítése előtt el kell végeznünk a magassági kiértékelést.

Ha már rendelkezésre áll kellő felbontású DTM az adott területről, úgy a pixelközéppontok Z koordinátáit a DTM felhasználásával interpoláljuk. Az ortofotó pixeleinek szürkeségi értékeit vagy azon képpixelek szürkeségi értékeivel tesszük egyenlővé, amelyekbe az átszámítás után esnek, vagy interpolációval határozzuk meg a négy legközelebbi pixelközépponthoz tartozó szürkeségi értékekből. A célból, hogy a transzformációból egy képpixel se maradjon ki az ortofotó pixelszámát a kép pixelszámához képest jelentősen meg kell emelni.

3.46 ábra - szines, nagyméretarányú ortofoto részlet

A digitális ortofotó a raszteres vagy hibrid GIS szoftverek egyik legfontosabb bemenő adata.

Fotogrammetriai munkaállomások

A digitális fotogrammetriai munkaállomások céljaira különleges felhasználói interfésszel és néhány speciális perifériával ellátott, gazdag grafikus feldolgozói és megjelenítési képességekkel rendelkező számítógépet alkalmazhatunk. A számítógépet az alkalmazott szoftver teszi fotogrammetriai munkaállomássá. Lényeges még, hogy a monitort valamilyen módszerrel sztereoszkopikusan lehessen szemlélni.

3.47 ábra - fotogrammetriai munkaállomás

A fentiek szerint a számítógép típusa elvileg nem meghatározó, az oktatási gyakorlatban találkozunk PC-ékkel is munkaállomás szerepkörben, gyakorlati, termelési feladatok megoldására azonban gazdaságosan csak a 'munkaállomás' kategóriájú számítógépek alkalmazhatók. A munkaállomások alkalmasságát a külön grafikus processzorok, a nagy műveleti sebességek (mind a képek, mind a vektor grafika, mind a számítások vonatkozásában) a képpufferek, a nagy belső és külső tárkapacitás, a memória közvetlen portok biztosítják.

Amint már említettük, ahhoz hogy a bármennyire is gyors, nagykapacitású számítógép alkalmas legyen az interaktív térkiértékelésre is arra van szükség, hogy ellássák sztereó felhasználói interfésszel.

A mesterséges sztereoszkopikus látás megköveteli, hogy a szemlélő a különböző felvételi pontokon készített, átfedő, tájékozott kép pár bal és jobboldali képét csak a bal illetve jobb szemével szemlélje. Ezt a feltételt a legkorszerűbb munkaállomások (pld. az alábbiakban ismertetett Intergraph IS 6487) úgy biztosítják, hogy másodpercenként 120-szor váltakozva hol a baloldali, hol a jobboldali képet vetítik a képernyőre. Mivel a sztereó látáshoz az kell, hogy az észlelő bal szeme mindig csak a bal, jobb szeme mindig csak a jobb képet lássa ezért olyan szemüveget adnak a kiértékelőnek, melynek bal 'lencséje' akkor sötétül el amikor a jobb kép van a képernyőn, a jobb 'lencséje' pedig akkor zár, amikor a képernyő a bal képet vetíti. A zárást a 'lencsékben' lévő folyadékkristályok segítségével érik el, melyek feszültség hatására elsötétülnek. A 'lencsékre' jutó impulzusok szinkronizálását úgy oldják meg, hogy a képernyő szinkronizáló jeleivel infravörös fényforrást modulálnak, mely a képernyő felől az észlelő felé sugároz. Ennek a kialakításnak az az előnye a vezetékes szinkronizálással szemben, hogy egyszerre több észlelő is szemlélheti a sztereó modellt aminek elsősorban az oktatásban van nagy jelentősége.

Ismerjük meg egy korszerű fotogrammetriai munkaállomás az INTERGRAPH ImageStation 6487 néhány fontosabb jellemzőjét. A számítógép architektúrája egyesíti a RISC munkaállomást a képfeldolgozó kompjuterrel, olyan párhuzamos felépítést hozva létre, mely biztosítja a raszteres és vektoros adatok egyidejű megjelenítését és manipulálását ugyanazon a képernyőn anélkül, hogy az átfedő vektoros állomány törölné vagy megváltoztatná az érintett pixeleket. E célból mind a képek mind a rajzok tároláséra olyan puffer kerettárolókat biztosít, melyekben a színek számára 24 bit áll rendelkezésre.

A VITec képfeldolgozó kompjuter sebessége 300 MOPS (300 millió műveletet hajt végre másodpercenként). A vektor grafikát az Intergraph EDGE II+ grafikus alrendszere csővezeték rendszerű feldolgozással 24 biten végzi, a vektor műveleteknél a CPU SPECmark-ja 33. A monitor 27 inch-es. 1664x1248 pixel felbontású.

A rendszer belső memóriája alapkiépítésben 32 MB ECC, mely 256 MB-re bővíthető. A merev lemez 1 GB-s. A nagymennyiségű be- és kimenő adatra figyelemmel a rendszer gyors SCSI buszán hat szabad port van, a lemez és szalagegységek bővítésére.

A munkaállomás UNIX V 3.1 operációs rendszerrel működik. A fotogrammetriai feladatokat az IMD moduláris program rendszer és moduljai segítségével hajtja végre. A feladat megfogalmazás, input output szervezés céljait az ISPM modul szolgálja. A fotogrammetriai alappont meghatározás illetve a tájékozás az ISDM és ISDO modulokkal végezhető. Az adatnyerést az MSFC program csomag hajtja végre s lehetőség van a nyert adatok közvetlen bevitelére az Intergraph GIS szoftverébe az MGE-be. Az interaktív (operátoros) kiértékelések magával az IDM-el végezhetők. Az automatikus DTM előállításhoz a más cégek által készített ISAT és ISMT programok használhatók. As ISIR program egy légifénykép és a tájékozási adatok illetve az MGE MSM moduljával nyert DTM segítségével hozza létre az ortofotót.

Az output alapvetően digitális ortofotókból áll, melyek megfelelő formátumban optikai lemezeken terjeszthetők és különböző GIS szoftverek számára jelentkezhetnek bemenetként. A vonalas kiértékelés eredményei vagy közvetlenül az MGE GIS szoftverbe jutnak magán az állomáson, vagy a MicroStation Feature Collection (MSFC) szerkesztő programból többféle formátumban más vektoros GIS rendszerekbe vihetők. Ha az eredményekből térképet akarunk rajzolni, úgy az MGE Map Publisher moduljával vezéreltethetjük a térkép szeparátumok vagy ortofoto térképek filmre írását valamely nagy formátumú MapSetter rendszeren. A további nyomdatechnikai munkák a szokásos módon végezhetők.