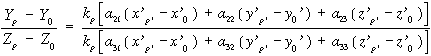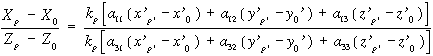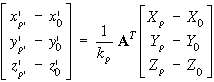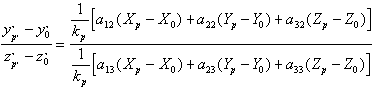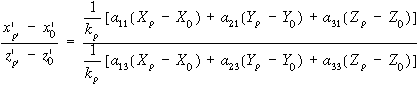Fotogrammetriai módszerek a pontok helyzetének meghatározására I

Az a gondolat hogy egyszerre a valóság számtalan látható részletét rögzítsük azután vált technikai realitássá, hogy 1839-ben W. Talbot angol fizikus felfedezte a fényképezést és hogy ugyanebben az évben I. N Niepce és I. L. M. Daquerre megalkották a polaroid ősét. Ahhoz hogy ezt a technikát a térképekhez hasonlóan a földfelszín felülnézetben történő ábrázolására használhassuk még arra is szükség volt, hogy felülről fényképezhessük le a földet, ez a feltétel a repülés fejlődésével teljesült. A század húszas éveitől kezdődően a légifényképezés iparszerű tevékenységgé vált.

A következő probléma az volt, hogy hogyan lehet a fényképekből torzításmentes vonalas térképet csinálni. Ezt a feladatot két lépcsőben oldották meg: az első szakaszban kifejlesztették a rajzasztallal összekapcsolt analóg sztereo kiértékelő berendezéseket, majd a második szakaszban, a 60-as évek közepétől, elkezdődött a digitális számítógépek bevonása a kiértékelő munka támogatására.

A másik irányzat a torzításmentes tónusos (fényképszerű) termék létrehozását célozta meg. Ez a törekvés is két állomáson keresztül jutott el a máig. A 70-es évek elejéig a viszonylag sík terepekről készíthető, optikai-mechanikai úton transzformált termékek alkalmazhatósági körét igyekeztek különböző fortélyokkal kiterjeszteni kevéssé sík terepekre, míg ezek után megjelent az ortofoto, mely gyakorlatilag tetszőleges domborzatú terepet képes torzítás nélkül fénykép formájában ábrázolni.

Napjainkra a különböző irányzatok, technikák, műszerek gyakorlatilag egybeolvadtak és átalakultak a digitális fotogrammetriai munkaállomásnak nevezett feltupírozott, speciális perifériákkal ellátott, gazdag szoftver választékú, munkaállomás osztályú számítógéppé. A fotogrammetriai feldolgozás tehát átalakult az optikai mechanikai berendezések manuális vezérléséből a feldolgozó programok vezérlésébe. Mivel nem lehet a célunk e rövid összefoglalásban egy vagy több feldolgozóprogram ismertetése az input és output felvázolása mellett a kettő között elhelyezkedő alap összefüggésekre igyekszünk a figyelmet fordítani.

Ennek megfelelően a fotogrammetriai összefoglaló első részében megismerkedünk

a bemenő adatok létrehozásával és
és a fotogrammetriai kiértékelés alapját képező legfontosabb geometriai és matematikai összefüggésekkel.

Bemenő adatok

A légi fotogrammetria bemenő adatai az analóg vagy digitális légifényképek.

A 3.27 ábrán egy részletet látunk egy északamerikai lakott település 1:24000 méretarányú légifényképéből. Meg kell jegyeznünk, hogy a hálózati bemutatás érdekében még a kivágott részletnek is csökkenteni kellett a felbontását.

3.27 ábra - 1:24000 méretarányú szines légifényképrészlet

Az analóg felvételeket a légi felvevő kamarák állítják elő, melyek a felvevő repülőgépekben kerülnek rögzítésre. A kamarák bonyolult automatikus rendszerek, melyek elemei a legmagasabb műszaki színvonalon kerülnek kialakításra. A kamarák feladata, hogy a repülési paraméterekhez (repülési magasság, repülési sebesség) kapcsoltan meghatározott időközökben, a megvilágítási körülményeknek, a sebességnek, a film érzékenységnek, stb. megfelelő időtartamra megvilágítsák a filmet.

E közben a kamara objektívje nagyfelbontású, nagy fényerejű, lencsehibákra korrigált, kis elrajzolású kell hogy legyen. A fényképezés pillanatában a filmnek szigorúan sík felületűnek kell lennie (ezt vákuumos leszívással érik el), és az előhívás, szárítás folyamatában eredeti alakját nem szabad megváltoztatnia.

3.28 ábra - Zeiss RMK TOP típusú légi felvevő kamara

A kamarák és film anyagok több évtizedes fejlődésének köszönhetően egyes típusaik ma már a legmagasabb követelményeket is kielégítik.

Minden légifényképre leképződnek a képkoordináta rendszer tengelyeinek végpontjai (általában ékek formájában) valamint a képek sarkain olyan jelek melyek távolságát nagy szabatossággal ismerik. Ha megmérjük e jelek közötti távolságot az előhívott képen az eredeti távolság ismeretében következtetni tudunk a képtorzulásra.

Amint a bevezetőben említettük napjaink fotogrammetriai feldogozása digitális fotogrammetriai munkaállomásokon megy végbe. Ezek a számítógépek pedig digitális formában várják az inputot. A digitális bemenő adatokat kétféle képen hozhatjuk létre: vagy digitalizáljuk a fényképet vagy analóg helyett digitális kamarát használunk.

Bár a fénykép digitalizálók nem olcsó berendezések napjainkban mégis inkább ezeket s hozzájuk kapcsolva a hagyományos légi felvételeket részesítik előnyben a szintén nem olcsó, de még nem teljesen kiforrott digitális légi kamarákkal készült digitális fényképekkel szemben.

Az egyik legelső korszerű légifénykép pásztázó berendezés a Zeiss művek PS1 PhotoScan típusjelű pásztázója. A műszer érzékelő eleme a 2048 darab szilicium alapú CCD (Charge Coupled Device) fényérzékelő félvezetőből álló sordetektor. Egy elem azaz egy pixel mérete 7.5 mm. A pásztázás szélessége 15.36 mm. Minden pixel elemhez egy byte tartozik az attributív információ, esetünkben a szürkeségi érték, tárolására. A sordetektor a pásztázás során mozdulatlan helyzetben van, az érzékelt képsorok változását a képtartó szakaszos mozgatásával érik el. A képtartó, miután az első pásztázási szélességben minden sor letapogatása megtörtént a pásztázási szélességnek megfelelően oldalt mozdul és folytatja a sorok letapogatást az új tartományban. Egy légifénykép (23x23 cm) letapogatása kb. 16 pásztázási tartományt igényel.

3.29 ábra - Zeiss PhotoScan TD tipusú képdigitalizáló

A légifényképet a képtartóba való behelyezéskor csak közelítőleg kell tájékozni, a pontos tájékozást azaz a képtartó kocsi koordináta rendszere párhuzamossá tételét a képkoordináta rendszerrel a berendezés automatikusan végzi. A 7.5 mm-es pixel méreten kívül nagyobb pixel méretek 15 mm, 30 mm, 60 mm, 120 mm is beállíthatók.

A 3.29 ábrán bemutatott szkenner a PS1 továbbfejlesztett változata. Érdemes megemlíteni, hogy a berendezéshez külön számítógépet kell hozzákapcsolni, mely 48 MB memóriával, 2 GB rendszerlemezzel, 4 GB adatlemezzel és 20 "- nál nagyobb monitorral rendelkezik.

Egy fekete-fehér légifénykép legnagyobb felbontású digitalizálása 20 percig tart és a memória igénye kb. 1 GB. A digitális légifelvevő kamarák legfőbb problémáját az előző mondat végén fogalmaztuk meg: amíg nagysebességgel írható optikai diszkeket nem illesztenek ezekhez a kamarákhoz addig gazdaságos, üzemszerű működésük nem képzelhető el, hisz a fényképezés akkor gazdaságos, ha a kijelölt területeket egy felszállással fényképezik le, ez pedig több száz kép elkészítésével is járhat.

3.30 ábra - a digitális sorkamara működési elve

Maguk a digitális kamarák vagy egyszerűbben szólva jó minőségű digitális fényképezőgépek két csoportba oszthatók. Az egyik csoport az előzőekben ismertetett szkennerhez hasonlóan sordetektorral érzékel de azzal a különbséggel, hogy nem az objektumot mozgatja a léptető motor hanem a detektort (3.30 ábra).

Az EIKONIX digitális kamara például 4096 elemmel rendelkezik a sordetektorban és a mozgás eredményeképpen 4096x4096 pixelből álló digitális képet hoz létre. Ezzel a megoldással azonban csak mozdulatlan objektumot fényképezhetünk mozdulatlan kamarával, azaz a mozgó repülőgépen ez a fényképezőgép nem alkalmazható. Ugyanakkor a megfelelő állványra szerelt kamarával digitalizálhatunk légifényképeket, igaz alacsonyabb pontossággal mint a speciálisan e célra szolgáló szkennerekkel.

A legfrissebb fejlesztésekben a jól ismert professzionális 6x6-os gépekhez digitális érzékelő hátszerkezetet fejlesztett ki a PHASE ONE dán cég. Bár a prospektusban egyáltalán nem írnak róla nagyon valószínű, hogy a 2000 x 2000 pixeles felbontáshoz sordetektort alkalmaznak.

Ugyanez a cég 1997 áprilisában piacra dobta a nagyformátumú stúdió fényképezőgépekhez illeszthető hátszerkezetét. Az érzékelő terület 7 cm. x 10 cm., a felbontás 6000 x 8400, egy digitális színes kép 144 MB méretű, a hátszerkezet ára 30 000 amerikai dollár.

3.31 ábra - a PHASE ONE dán cég digitális érzékelője a Rollei tipusú 6x6-os fényképezőgéphez

3.32 ábra - a PHASE ONE dán cég digitális érzékelője a Hasselblat tipusú 6x6-os fényképezőgéphez

A jövő légifotogrammetriára is alkalmas kamarái feltehetőleg a digitális mátrix (keret) kamarák (angol nevük és rövidítésük Digital Frame Camara DFC) közül fognak kikerülni. Ezekben a kamarákban a félvezető detektor fényérzékeny elemei úgy nevezett fotóhelyei nem sorban hanem mátrixban helyezkednek el. Az egyszerűbb típusoknál a kb. 1024x1024 fotóhellyel rendelkező szilícium alapú félvezető chip-detektor 8 bites jelet állít elő. Ebben a kategóriában már 10000 $ alatt is lehet fényképezőgépet kapni. Léteznek már 4000x4000 fotohellyel rendelkező kamarák 10-16 bites jellel is, ezek ára azonban figyelembe véve az adatátvitel és tárolás eszközeit is ma még nagyon magas.

A digitális kamarával történő légifényképezés egyelőre még kísérleti stádiumban van pillanatnyilag úgy tűnik, hogy az előnyök elsősorban a távérzékelési hasznosítás terén jelentkeznek. Az érzékelők ugyanis szélesebb hullámtartományra érzékenyek mint a negatív anyagok s ez lehetőséget biztosít megfelelő színszűrők alkalmazása esetén közel ugyanazon terület különböző hullámhosszúságú sugárzásának rögzítésére azaz szakkifejezéssel élve multispektrális felvételek készítésére.

A fotogrammetriai alkalmazás szempontjából a keret kamarák előnye, hogy a kapott kép kontrasztosabb és részletgazdagabb a hasonló objektívval előállított fényképeknél, s az hogy a képek jelen időben szemlélhetők a monitoron, lehetőséget biztosítva az esetleg szükséges korrekciók azonnali alkalmazására a fényképezési folyamatban. További előny hogy a kamarák belső geometriája hasonló a hagyományos kamarákéhoz s így az ismert algoritmusok használhatók. Ez utóbbi állításhoz azt a kiegészítést kell tennünk, hogy a keret kamarákat azért hívják keret kamaráknak mivel a detektor mátrix szélső fotóhelyei egyértelműen meghatározzák a kép keretét. A számítógép a képet függetlenül a detektor cellák esetleges méretdifferenciáitól szabályos raszterbe képezi le.

A szabályos raszter középvonalai egyértelműen meghatározzák a képkoordináta rendszert, ezért a keret kamarákban nincs szükség keretjelekre. Ha a detektor mátrix geometriai felépítése a pontossági határokon belül szabályos, úgy a számítógépben létrejött szabályos kép az eredeti raszter képpel azonosnak vehető. Ellenkező esetben egy szabályos rács lefényképezésével határozzák meg azokat a korrekciókat, melyekkel a feldolgozás folyamatában az egyes pixeleket el kell látni.

A jelenleg használatos digitális kamarák legnagyobb hátránya, hogy a mátrix kis területe következtében kicsi a látószög és kicsi a lefényképezett terület. Példaképpen megemlítjük, hogy a KODAK MEGAPLUS mod. 1.4 keretkamara esetében a detektor egy 8.98 mm. x 7.04 mm.-es CCD chip, mely vízszíntes értelemben 1320, függőleges értelemben 1035 fotohelyet tartalmaz, a pixelek 6.8 µm. oldalhosszúságú négyzetek. Ha az objektív gyujtótávolsága 15 mm., úgy a látószög vízszíntes értelemben 16.7°, magassági értelemben pedig 13.2°. Ez azt jelenti, hogy 300 m.-es repülési magasság esetén a leképezett terület 180 m. x 150 m., 11000 m. esetén pedig 6600 m. x 5175 m.

3.33 ábra - a KODAK KAF-6300 tipusú hátszerkezete a CCD mátrixszal

3.34 ábra - KODAK DCS 460 tipusú digitális kamera

Az 1996-ban kifejlesztett KODAK KAF-6300 tipusjelű legkorszerűbb mátrix CCD szenzor mérete 18.4 mm. x 27.6 mm., 3060 x 2036 négyzet alakú fotohelyet tartalmaz. A szenzort hátszerkezetként illesztik a népszerü kisfilmes tükörreflexes fényképezőpgépekhez (NIKON, CANON). Ezek a kamarák már jól használhatók a földi mobil felmérő rendszerekben

Néhány geometriai, matematikai összefüggés

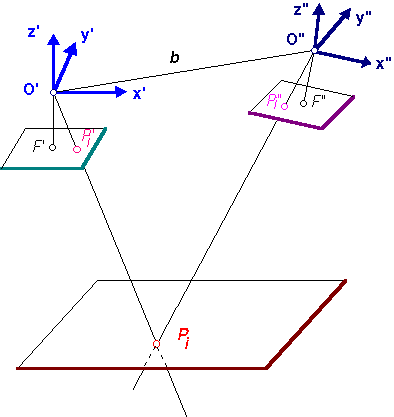
A fényképezés geometriai modellje a centrális perspektíva. Ebben a modellben a tárgyképről kiinduló vetítősugarak egy pontban a vetítési középpontban találkoznak. A vetítősugarak metszéspontjai a képsíkkal a képpontok. Ha a vetítési középpont a tárgysík és a képsík között helyezkedik el akkor negatív képet kapunk. Az ellenkező helyzet felel meg a pozitív képnek.

A vetítési középpontból a képsíkra bocsátott merőleges a kamara tengely. A kamarákat úgy igyekeznek kialakítani, hogy a kamara tengely metszéspontja essen egybe a képkoordináta rendszer x'', y 'tengelyeinek metszéspontjával, mivel ez a gyakorlatban nem sikerül abszolút pontossággal a metszéspont koordinátáit
(x₀', y₀', -z₀'=f ) a kép belső adatainak nevezik és figyelembe veszik a számítások során. A z₀' negatív előjele abból adódik, hogy a 3.35 ábra szerint a térbeli képkoordináta rendszer kezdőpontját jelentő vetítési középpontot a kép fölött vettük fel, azaz pozitív képekkel dolgozunk.

3.35 ábra - a kép belső adatai

A centrális vetítés eredményeképpen előállt egyetlen fényképből csak akkor tudjuk helyreállítani a tárgy mérethelyes eredeti alakját (illetve a tárgy határvonalait meghatározó koordináták eredeti értékét), ha a tárgy síkidom volt és ismerjük mind a tárgysík mind a képkoordináta rendszer elhelyezkedését valamely ismert koordináta rendszerben. Egyszerűség kedvéért a tárgysíkot azonosnak vagy párhuzamosnak tekintjük a földhöz kapcsolt geodéziai koordináta rendszer XY síkjával és ekkor a rendszer merevségét a képkoordináta rendszer elhelyezkedését leíró külső adatok biztosítják.

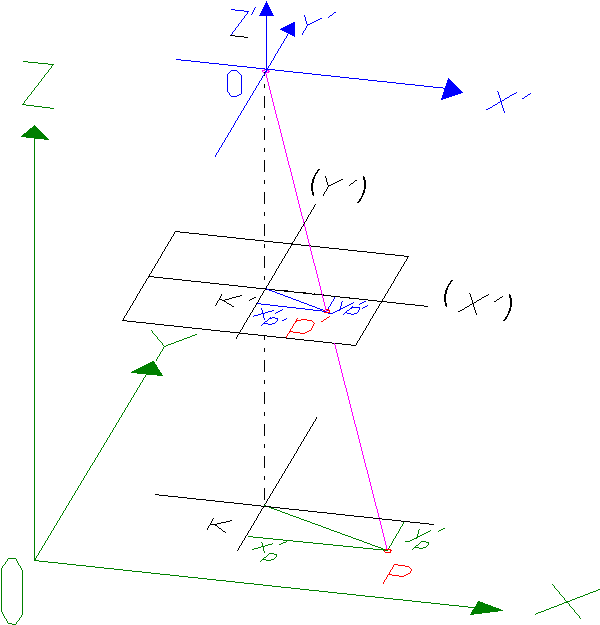
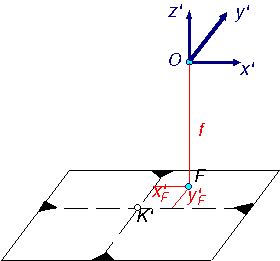
A 3.36 ábrán felvázoltuk a külső adatok két lehetséges megadását.

Rajztechnikai okokból negatív képet vettünk fel, ez azonban a külső adatok megadásán nem változtat.

A fénykép helyzetét a földhöz rögzített háromdimenziós koordináta rendszerhez képest hat adattal adjuk meg, három koordinátával és három szöggel. A három koordináta a vetítési középpont három koordinátája X₀, Y₀, Z₀.

Rajzunkon azt az egyszerű esetet mutatjuk amikor X₀=Y₀=0.

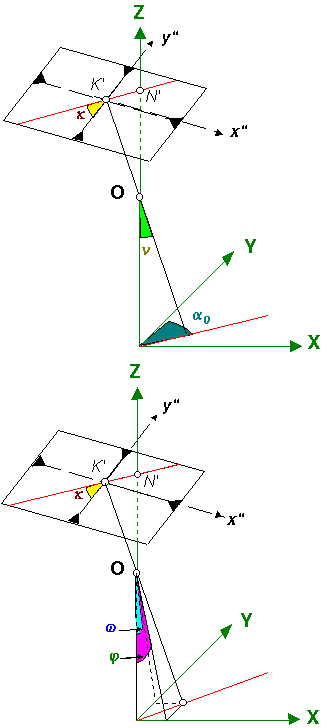
3.36 ábra - a külső adatok megadásának két szokásos módja

A három szögkomponens közül kettő megadására két lehetőségünk is van: az első lehetőség, hogy megadjuk a kamara tengely szögét a függőleges Z tengellyel -t, valamint a kamara tengelyen átfektet függőleges síknak az XY síkkal alkotott metszésvonalának irányszögét (azt a szöget amivel az Y tengelyt pozitív értelemben a kérdéses vonalba forgatjuk) -t; a második esetben felbontjuk a kamara tengely dőlését egy hosszirányú komponensre () és egy keresztirányú komponensre ().

A harmadik szögkomponens mindkét esetben ugyanaz: a fénykép elfordulása a kamaratengely körül amit a kamaratengelyen át fektetett függőleges sík képsíkkal való metszésvonalának az y" tengellyel bezárt szögével -al fejezünk ki.

Az y" tengely nem más mint az előzőekben már megismert y' tengely vetülete a képsíkon.

A külső adatok (vagy külső tájékozási adatok) tehát összekapcsolják a földhöz kötött nagybetűs koordináta rendszert a képhez kötött vesszős koordinátarendszerrel, s ezen keresztül a belső adatokkal. Ebből következik, hogy ha ezek az adatok ismertek és ismertek egy tetszőleges pont koordinátái az egyik rendszerben, úgy kiszámíthatjuk ugyanennek a pontnak a koordinátáit a másik rendszerben.

A két koordináta rendszer kapcsolatát matematikailag az alábbi egyenlet tartalmazza:

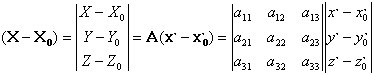Nem nehéz észrevenni a hasonlóságot a referencia rendszerek transzformációjával a különbség a jelöléseken kívül mindössze abban van, hogy a mostani koordináta transzformációban mindkét rendszer méretarányát azonosnak tekintjük.

3.37 ábra - forgatások értelmezése

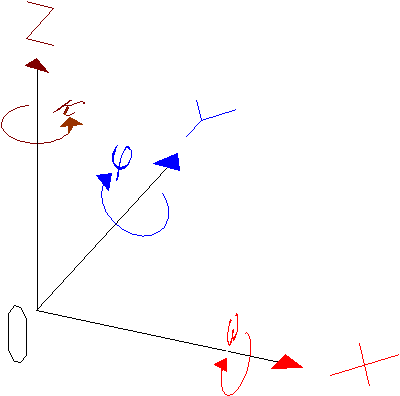
Ha a forgások a repülőgép tengelyei mentén mennek végbe és sorrendjük: (orr és farok által meghatározott tengely dőlése), a szárnyak dőlése (csűrés), a jobbra vagy balra kanyarodás (3.37 ábra) akkor a forgatási mátrix:

alakban írható fel (a fenti) kifejezés azért tér el a transzformációval kapcsolatban megismert forgatási mátrixtól mivel más a szögek értelmezése: és más az egymás utáni forgatások sorrendje).

Az adatnyeréshez azonban nem arra van szükségünk, hogy ugyanazon földi vagy képpont különböző rendszerbeli koordinátáit ismerjük, hanem arra, hogy a képpontok képkoordináta rendszerbeli koordinátáival kifejezzük a megfelelő földi pontok koordinátáit a földhöz kapcsolt koordináta rendszerben. Ha ugyanis ilyen összefüggések a rendelkezésünkre állnak, úgy megfelelő számú lefényképezett, ismert koordinátájú földi pont felhasználásával meghatározhatjuk a kép(ek) tájékozási adatait és ezek segítségével újabb lefényképezett pontok földi koordinátáit.

Már itt meg kell említenünk, hogy ahhoz, hogy egy földi pont mindhárom koordinátáját meghatározhassuk a kérdéses pontnak legalább két tájékozott képen rajta kell lennie.

Az összefüggés megkeresése érdekében a 3.38 ábrán párhuzamossá tettük a képkoordináta rendszert a földhöz kapcsolt koordináta rendszerrel, azaz beszoroztuk a képkoordinátákat a forgatási mátrixszal. Ebben a helyzetben a Z' tengelyre a P pontra és P' képére illeszkedő derékszögű háromszög segítségével felírható hogy a földi pont koordinátái és a megfelelő képkordináták arányosak azaz

és a földi pont koordinátái:

A fenti egyenletben szereplő k_p arányossági tényező sajnos pontonként változik ezért a kifejezés a tájékozási elemek kiszámítására csak az arányossági tényező kiküszöbölése után használható.

3.38 ábra - kapcsolat a földi pont és képi megfelelője között párhuzamossá tett koordinátarendszerekben

Bontsuk fel a vektoregyenletet a koordinátánkénti egyszerű egyenletekre és osszuk el mind az X mind az Y kifejezést a Z koordináta kifejezésével:

Egyszerűsítsünk az arányossági tényezővel és jelöljük az első egyenlet számlálóját SZ_x-nek a másodikét pedig SZy-nak, legyen a közös nevező N, akkor

A tájékozási adatok meghatározásához általában a képkoordinátákat fejezik ki. Ekkor az előzőekkel analóg módon a következő kifejezéseket kapjuk:

;

Ha még egyszer megnézzük a 3.37 ábrát, akkor minden különösebb magyarázat nélkül beláthatjuk, hogy kapott kifejezések azt a geometriai tényt írják le, hogy a pont és képe egy egyenesen van, ezért a kérdéses egyenleteket kollinearitási feltételeknek hívjuk. Az utolsó két egyenletünk tartalmazza mind a belső mind a külső adatokat, e mellett egy földi pont és képi megfelelője földi illetve képi koordinátáit. Ha tehát ismerjük 3 lefényképezett földi pont koordinátáit, képkoordinátáit pedig most nem részletezett módon a fényképről lemérjük, ismerjük (korábban már meghatároztuk) továbbá a belső adatokat, úgy elvileg semmi akadálya annak, hogy a külső tájékozás adatait kiszámítsuk. Sajnos azonban az egyenletek nem lineárisak, ezért a megoldás csak sorba fejtéssel és iterációval történhet.

A sorba fejtéshez szükségünk van az ismeretlenek előzetes értékeire. Minél jobbak az előzetes értékek annál kevesebb iterációra van szükség. Az előzetes értékeket a légifényképen található adatokból, a repülési tervből és a repülés körülményeiről készített jegyzőkönyvből határozhatjuk meg, bár újabban egyre több olyan kísérletről olvashatunk, melyekben a külső adatokat részben (csak a vetítési pont koordinátáit), vagy egészben (a szögadatokat is) egy vagy több a repülőgépre szerelt GPS vevővel határozzák meg. Nem kell nagy jóstehetség annak a prognosztizálására, hogy ez a módszer egyre inkább terjedni fog, sőt az is várható, hogy a GPS technikában rejlő képességek jobb kihasználásával, szerényebb pontossági igények esetén magát a kiértékelést is csupán ezekre az adatokra támaszkodva földi illesztő pontok nélkül fogják végrehajtani.

A számítástechnika alacsonyabb fejlődési szintjén komoly problémát jelentett a kollinearitási feltételek felhasználásával számítani a több átfedő képet tartalmazó nagyobb rendszereket, mivel a megoldást szolgáltató egyenletrendszer esetenként több száz ismeretlent is tartalmazott. Az egyenletrendszer méretének csökkentése érdekében a feladatot két részre bontották: előbb létrehoztak egy olyan helyzetet, mely hasonló volt a két átfedő kép kölcsönös helyzetére a felvétel készítés időpontjában, majd az így nyert úgy nevezett modellkoordinátákat a térbeli hasonlósági transzformációval áttranszformálták a földhöz kapcsolt koordinátarendszerbe. Bár a modellmódszerek jelentősége egyre jobban csökken, geometriai alapjait érdemes megismerni, mivel azok felhasználásra kerülnek az automatikus magasságkiértékelést előkészítendő a kép-pár normál-sztereogrammá transzformálásában, e mellett pedig alkalmasak lehetnek a GPS segítségével meghatározott szögadatok pontosítására is.

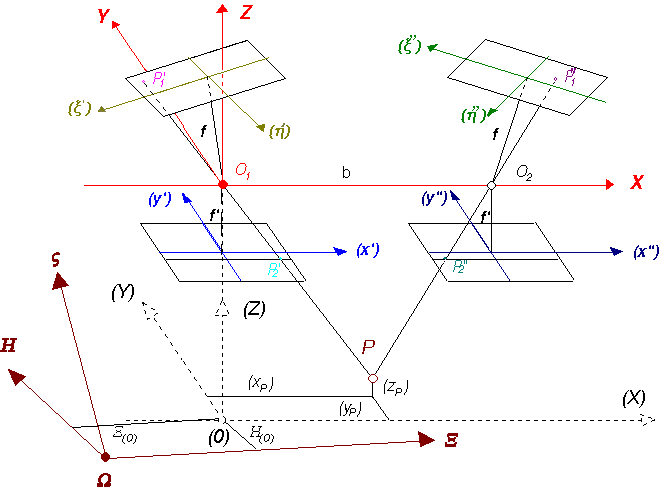
A 3.39 ábrán feltüntettünk egy, a két kamara fényképezéskor elfoglalt kölcsönös helyzetéhez hasonló helyzetet. Azért csak hasonló és nem azonos a két kölcsönös helyzet, mivel a képek egymástól mért távolága (a b távolság x' irányú komponense) tetszőleges lehet.

3.39 ábra - képpár kölcsönös helyzete

Az ábrából világos, hogy a fényképezés pillanatában a megfelelő képpontokat az optikai középpontokkal összekötő egyenesek a tárgypontban metsződnek. Ha legalább 5 megfelelő képpontpárra felírjuk ezt a feltételt, úgy a sorbafejtések és iterációk miatt elég bonyolult számításokból megkapjuk a két képkoordinátarendszer kölcsönös helyzetét meghatározó szög-, és b_y^I-II, b_z^I-II hossz- tájékozási adatokat. Amint már említettük b_x^I-II elvileg önkényesen vehető fel. Ha azonban GPS rendszerrel már megmértük valamennyi vetítési középpont abszolút koordinátáit és valamennyi , , szöget az exponálási helyeken, úgy célszerű mind a közelítő értékeket mind a szabad báziskomponenst ezekből számítani.

A kölcsönös tájékozásból nyerhető feltételi egyenletek jelentős mértékben megjavíthatják a GPS-el meghatározott külső adatokat, s ezzel a közelítő kiértékelés pontosságát. További előnye a módszernek, hogy nem igényel földi méréseket valamint az, hogy a korszerű rendszerekben a megfelelő képpontok koordináta meghatározása gyakorlatilag automatikusan történik.

Amint említettük a digitális formában tárolt képpárt a kölcsönös tájékozás felhasználásával is normálsztereogrammá tudjuk alakítani. A normálsztereogramm kifejezés olyan speciális elhelyezkedésű képpárt takar, melyek x' és x'' tengelyei egybeesnek a bázissal, z' és z'' tengelyei pedig a megfelelő kamaratengelyekkel (3.40 ábra).

Normálsztereogramm esetén a megfelelő képpontok y koordinátái azonosak (vagy ahogy a fotogramméterek mondják nincs harántparallaxis) és ennek következtében egyszerűbb a megfelelő pontok automatikus azonosítása.

3.40 ábra – kép-pár átalakítása normál-sztereogrammá

Mielőtt azonban erre rátérnénk néhány magyarázattal tartozunk a 3.40 ábrával kapcsolatban majd röviden összefoglaljuk a kölcsönös tájékozást és normalizálást leíró kifejezéseket. A téma részletei iránt érdeklődők a [7] tankönyvből nyerhetnek eligazítást.

Az ábrán látható X,Y,Z koordinátarendszer a normál-sztereogramm létrehozására szolgáló modell-koordináta rendszer. (Tulajdonképpen két olyan koordinátarendszerről van szó, melyek Y és Z tengelyei párhuzamosak, X tengelyük közös, kezdőpontjaik pedig a b bázistávolságra helyezkednek el egymástól).

Az eredeti képek szintén a két vetítési középpont alatt helyezkednek el, az ábrán azonban az áttekinthetőbb ábrázolás érdekében negatív tükörképüket rajzoltuk meg. Ezért mutatnak mindkét képen az , képkoordináta tengelyek képi vetületei (), () az ellentétes irányba.

Végül meg kell említenünk a pontozott vonallal jelölt koordináta rendszert is, melyet úgy kapunk, hogy a modell koordináta rendszert önmagával párhuzamosan a Z tengely mentén mindaddig süllyesztjük, míg (O) nem illeszkedik a lokális referencia rendszer síkjára. Általános esetben az (X) (Y) sík nem esik egybe a lokális referencia rendszer síkjával a síkkal ezért az eredményül kapott modellkoordinátákat még hasonlósági transzformációval át kell alakítani lokális referencia rendszerbeli koordinátákká.

Ha azonban GPS segítségével megmértük az exponálási helyeket (ismertek ), úgy a b bázis a koordinátákból kiszámítható azaz a modell méretaránya megközelíti a fényképezésnél fennállt tényleges helyzetet. Ha e mellett a repülési magasság is állandó volt azaz , úgy a modell módszer a valódi magasságok közelítő értékeit szolgáltatja.

A kölcsönös tájékozás segítségével a két kép kölcsönös helyzetét meghatározó öt adatot határozhatunk meg. A 3.38 ábrán feltüntetett helyzet kapcsán (amikor a modellkoordináta rendszert azonosnak tekintjük az első kép koordinátarendszerével) három szög és két hossz komponens meghatározási lehetőségére utaltunk. Ha azonban a modell koordinátarendszert a 3.40 ábra szerint vesszük fel, úgy öt szögadat meghatározására nyílik lehetőség. Míg az előző esetben a második kép három tengely mentén történő elfordulását vizsgáltuk az első képhez képest, addig most mindkét kép elfordulásait akarjuk kiszámítani a speciálisan felvett modellkoordináta rendszerhez képest. Mivel azonban ez hat adatot igényelne a meghatározható öt adattal szemben feltételezzük, hogy az első kép X tengely körüli elfordulása Közel függőleges tengelyű felvételek esetén levezethető (lsd. [7]), hogy az alábbi kifejezés írható fel a megfelelő pontok képi megfelelőinek koordinátáira:

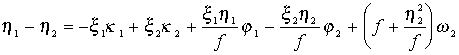Bár öt darab ilyen típusú egyenletből az ismeretlenek kiszámíthatók a gyakorlatban a feladatot 7-9 pont felhasználásával kiegyenlítéssel szokták megoldani.

Ha a forgatási mátrix elemeit mindkét eredeti digitális képre ismerjük, úgy a transzformált normál-sztereogramm megfelelő képét a kollinearitási feltételekbe történő behelyettesítés eredményeképpen nyert alábbi képletek segítségével hozhatjuk létre:

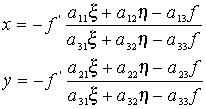A fenti képletben szereplő a_ij együtthatók a kérdéses képre számított forgatási mátrix elemei. Az f' értéket célszerű az eredeti képek fókusztávolságánál nagyobbra választani, hogy egy pixel se vesszen el a transzformáció során.

A közölt kifejezésekből az eredeti képek sarokpontjainak transzformálásával meghatározhatjuk az új képmátrixokat, de egyelőre még nem ismerjük az új pixelek szürkeségi értékeit (ha ugyanis az átalakítást a hivatkozott képletek felhasználásával az eredeti képek pixelei szerint végeznénk olymódon hogy minden pixel középpontját leképeznénk a normalizált képmátrixra és hozzárendelnénk az eredeti szürkeségi értéket, úgy nem kapnánk egyértelmű megoldást, mivel a normalizált képen a leképzés után egyes pixelek két szürkeségi értéket is kapnának, míg mások egyet sem).

A fenti problémák elkerülhetők, ha a létrehozott normalizált képmátrixok pixeleinek középpontjait meghatározzuk és visszavetítjük az eredeti képre. Ehhez azonban az szükséges hogy rendelkezzünk a visszavetítést leíró összefüggésekkel is, melyek az alábbi formában írhatók fel:

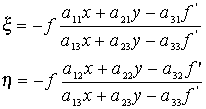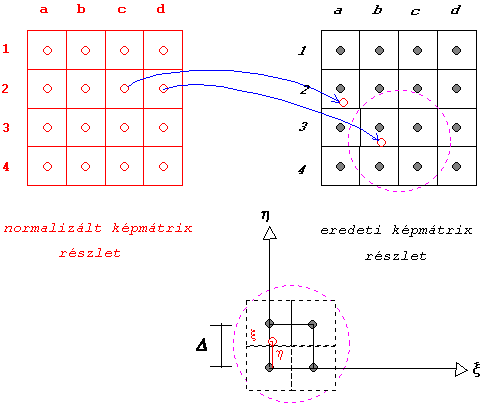
A visszavetítés eredményeképpen a normalizált kép pixelközéppontjai a 3.41 ábra tanulsága szerint általában nem esnek egybe az eredeti kép pixelközéppontjaival.
normalizált képmátrix szürkeségi értékeinek meghatározása ezután legegyszerűbben úgy történhet, hogy megnézzük melyik pixelközépponthoz van legközelebb az átvetített pont (azaz melyik pixelbe esik az eredeti képen) és ennek a pixelnek a szürkeségi értékét rendeljük a normalizált kép figyelembe vett pixeléhez.

3.41 ábra - normalizált képmátrix szürkeségi értékeinek meghatározása

Bár ez a módszer igen kevés futásidőt igényel, hátránya hogy kedvezőtlen esetben egy pixelnyi eltolódást is előidézhet a normalizált képen. Ezt elkerülhetjük a bilineáris (mindkét tengely szerint lineáris) interpoláció alkalmazása esetén.

Vizsgáljuk meg a 3.41 ábra normalizált képmátrix részletének 2d pixelét. Transzformálás után a pixelközéppont az eredeti kép 3b pixelének alsó részére kerül a középvonaltól kissé jobbra. Vegyünk fel egy koordináta rendszert, mely tengelye átmegy a 4c és 4b, tengelye pedig a 4b és 3b pixelek középpontjain. Jelöljük ebben a rendszerben az átvetített középpont koordinátáit -vel és -val, a pixel középpontok távolságát -val, az ij pixel szürkeségi értékét pedig sz_ij-el. A kérdéses pont szürkeségi értéke ezek után az alábbi képlettel számitható:

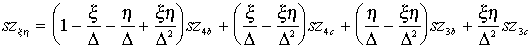A normalizálásra azért volt szükségünk mivel így egy dimenziós korrelációval határozhatók meg egy tetszőleges tereppont két képének koordinátái. A normalizálás elvégezhető az abszolút tájékozási elemek ismeretében is. Ekkor azonban az eredeti képek sokkal erősebb deformációt szenvednek az átalakítás során, ami óhatatlanul az automatikus kiértékelési pontosság csökkenéséhez vezet, ezért célszerűbb a további transzformációkat a már kiértékelt modellkoordinátákon végrehajtani.

Ahhoz, hogy megértsük, mire használhatók ezek a koordináták a 3.40 ábra segítségével felírjuk a modell ( abszolút tájékozás esetén a terep) és a képkoordináták egyszerű kapcsolatát a normál-szterogrammban:

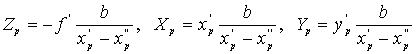Nem igényel külön magyarázatot, hogy a helyi referencia rendszer egy pontjára illeszkedő (X), (Y), (Z) koordinátarendszerben .

Az automatikus eljárásnak az a célja, hogy bizonyos rendszerben meghatározzák az ugyanazon földi pontokhoz tartozó x' és x'' koordináta értékeket a normalizált képpáron. Az összetartozó koordináta értékek meghatározására az egy dimenziós korrelációt használják.

A korreláció lényege, hogy a számítógép kiválaszt az első képen megadott pixelt megelőzően és követően meghatározott számú pixelt (sorszámával és szürkeségi értékével) ez a halmaz lesz a cél vagy minta állomány. A következő lépésben a második kép megfelelő sorában kiválaszt egy a cél állománynál nagyobb keresési állományt ( elvileg az egész második sort keresési állománynak tekinthetjük, a gyakorlatban a folyamat soron belüli előrehaladásával a gyorsabb futásidő érdekében igyekeznek korlátozni az állományt). Ezután a két állomány kölcsönös helyzetét változtatva (a minta állományt egy-egy pixellel eltolva) kiszámolják a két állomány korrelációs együtthatóját az egyes helyzetekre. Akkor 'toltuk' pontosan a második kép első képpel homológ pixelei alá a mintaállományt, amikor a korrelációs együttható a legnagyobb. Ebben a helyzetben szolgáltatja a minta állomány középső pixele felett lévő pixel koordinátája a keresési állományban a keresett x_P" értéket.

A korrelációs együtthatót (lsd. részletesebben pld. az [5]-ben) az alábbi kifejezésből számolhatjuk:

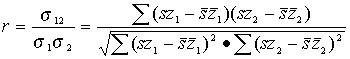ahol a minta állomány, pedig a mintaállomány aktuális helyzetének megfelelő keresési állomány rész szürkeségi értékeinek számtani közepe.

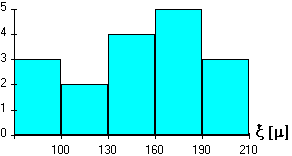
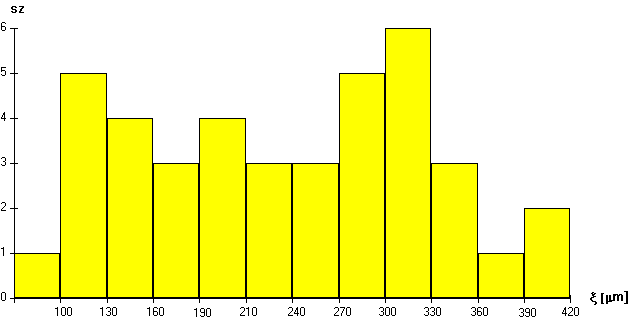
A 3.42-es ábrán feltüntettünk egy öt pixelből álló mintaállományt az első képről, a 3.43-as ábrán pedig a kijelölt keresési állományt a második képről. A pixel méretet mindkét esetben 30 mikrométernek választottuk.

A korreláció számításához induljunk ki abból a helyzetből amikor a minta állomány bal szélső pixele egybeesik a keresési állomány bal szélső pixelével (kényelmi okokból mindkét állomány bal szélső pixelét azonos koordinátájúnak választottuk), a következő lepésben egy pixellel jobbra toljuk a minta állományt, s az eltolást mindaddig folytatjuk amig a minta állomány jobb szélső pixele fedésbe nem kerül a keresési állomány jobb szélső pixelével.

3.42 ábra - mintaállomány

3.43 ábra - keresési állomány

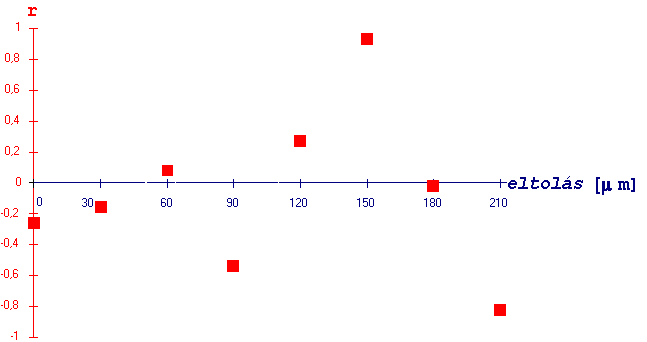
Minden helyzetben kiszámítottuk a korrelációs együtthatót és az eredményt a 3.1 táblázatban illetve a 3.44 ábrán tüntettük fel.

eltolás [mm]	0	30	60	90	120	150	180	210
r	-0.26024	-0.15724	0.08006	-0.53932	0,26906	0,93026	-0,0225	-0,82476

3.1 táblázat - korrelációs értékek

3.44 ábra - korrelációs értékek a minta állomány eltolásának függvényében

Mind a 3.1 táblázat mind pedig a 3.44 ábra alapján világos, hogy a korrelációs együttható az ötödik eltolás alkalmával a legnagyobb, azaz az első képen a 130-160 mm sarokponti illetve 145 mm középponti koordinátákkal jellemzett pixel megfelelője a második képen 270-300 mm sarokponti illetve 285 mm középponti koordinátákkal jellemezhető.

A módszer még tovább finomítható, ha kiegészítő információként még figyelembe vesszük a szürkeségi értékek változásait is a minta tartományban. Ideális esetben a minta állomány és a keresési állomány megfelelő pixelei azonos szürkeségi értékkel kellene, hogy rendelkezzenek. A valóságban azonban a pixelenkénti eltolással végrehajtott korreláció számítás eredményeképpen létrejött helyzetben ez nem áll fent. Ez részben azzal magyarázható, hogy az összhang még további pixelméret alatti eltolást igényel, részben a szürkeségi értékek véletlen és szabályos eltéréseivel a két képen. E tényezők figyelembe vételével, a már említett többletinformációt is felhasználva a pixelméret alatti eltolás kiegyenlítéssel számítható [7].

· a következő részben folytatjuk a fotogrammetriai adatnyerés tárgyalását, megismerjük a fotogrammetriai adatnyerés termékeit

· esetleg visszatérhet az előző részhez

· illetve a tartalomjegyzékhez

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc
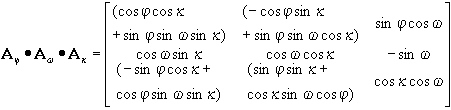
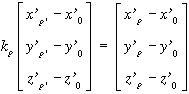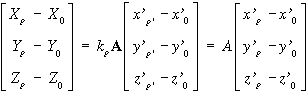