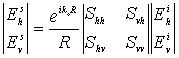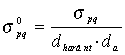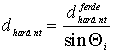Távérzékelés I

Ebben a részben megkezdjük az távérzékelés tárgyalását. Ezen belül megismerkedünk

az ürtávérzékelés fogalmával,
a különböző szenzortipusokkal,
részletesebben a radaros szenzorokkal ; végül
a rádiometrikus korrekció fogalmával.

Távérzékelés

A távérzékelés szó használata az első Landsat műhold 1972-es üzembelépésével vette kezdetét. Ha a szó betű szerinti értelmét kívánjuk megfejteni, akkor a távérzékelés alatt olyan adatnyerési eljárásokat értünk, melyek az adatokat a vizsgált objektummal létrehozott közvetlen, fizikai kapcsolat nélkül produkálják. Ha belegondolunk a meghatározásba, úgy nem nehéz rájönnünk, hogy ebben az értelemben távérzékelési technikák már jóval a mesterséges holdak létrehozása előtt működtek, hiszen például az asztrofizikai vizsgálatok az űrtechnikák megjelenése előtt még csak nem is gondolhattak a csillagok közvetlen mintavételezésére. Az információt az égitestek állapotáról, az ott lezajló folyamatokról különböző hullámhosszú rezgések továbbítják földünkre. Ezek a rezgések vagy a kérdéses égitesten végbemenő termonukleáris, vegyi stb. folyamatok termékei, vagy valamely más égitest által kibocsátott hullámok visszaverődései.

Ha a térbeli adatnyerés oldaláról vizsgáljuk a kérdést, a fotogrammetria mindenben megfelel a távérzékelés betűszerinti értelmezésének. Mégis a tényleges szóhasználat alapvetően két kritériumhoz kapcsolja a távérzékelés terminust: ugyanazt a jelenséget kettő vagy több tartományban mérjük, és/vagy mesterséges holdról hajtjuk végre az észlelést. Ez tehát azt jelenti, hogy ha a repülőgépen multispektrális felvételeket készítünk, akkor légi-távérzékelésről beszélünk, ha űreszközről (mesterséges hold, űrállomás, ürsikló) készítjük a felvételeket függetlenül attól, hogy egy vagy több hullám tartományban a módszer neve űrtávérzékelés.

Az űrtávérzékelés legfontosabb jellemzője, hogy hatalmas adattömeget tud automatikus rendszerben a földre továbbítani. Az érzékelő műholdak pályaelemeiktől függő gyakorisággal letapogatják a föld felületét, s az ugyanarra a területre vonatkozó ismételt felvételek megléte megteremti a multitemporális analízis lehetőségét. A másik fontos jellemző hogy a legtöbb űrtávérzékelő eszköz lehetőséget biztosít a multispektrális felvételek készítésére, melyek segítségével kisebb nagyobb megbízhatósággal a felszíni alakzatok bizonyos tulajdonság jellemzők egyezése alapján osztályokba sorolhatók. A létrejött osztályok tematikus fedvényként átvihetők a GIS-be.

Míg a légifényképezés rendszerint csak a földfelszín által visszavert illetve a felszín saját sugárzását felhasználva készíti a felvételeket (ez az úgy nevezett passzív letapogatás), addig sok távérzékelő űreszköz saját maga által kibocsátott sugárzás segítségével is képes a földfelszín letapogatására. Ezt a módszert aktív letapogatásnak, az eredményül kapott képeket radar képeknek nevezik. A radaros módszereknek az a nagy előnye, hogy olyan hullámhosszakat használnak, melyeket a felhőzet kevéssé nyel el, e mellett függetlenek a felszín megvilágítottságától, azaz a felvételek minősége nem függ az időjárástól és a napszaktól.

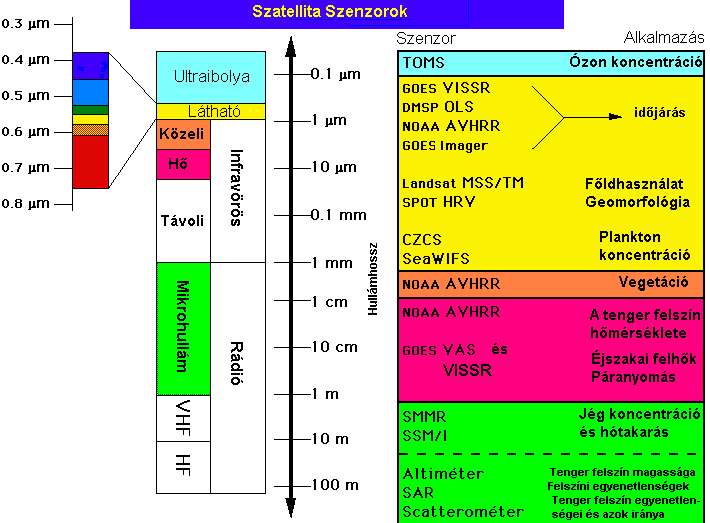
3.54 ábra - az elektromágneses hullámok spektruma és néhány szenzor a felhasználási terület megnevezésével

A 3.54 ábrán bemutattuk az elektromágneses hullámok spektrumát és felsoroltunk néhány szenzor típust a hozzátartozó felhasználás rövid megnevezésével.

Rögtön el kell mondanunk, hogy a kiválasztott példákon kívül valamennyi hullámtartományban számtalan másik szenzor típust is megnevezhettünk volna. A továbbiakban, a műholdak és termékek ismertetésekor ezt részben meg is tesszük. A korlátozás arra utal, hogy kizárólag a képalkotó szenzorokkal fogunk foglalkozni (nem térünk ki a tengerek magasságát mérő altiméterekre, vagy a tenger felszín szélviszonyait mérő scatterométerekre, stb.) és elsősorban a nagyobb felbontású térképészeti célú érzékelőket ismertetjük.

Ez nagyjából egybeesik azzal a szándékunkkal is, hogy igyekszünk redukálni azokat a globális szempontból ugyan nagyon fontos, de hazai vonatkozásban kevéssé releváns ismereteket, melyek az óceánok, a jég és hó és a trópusok monitorozására vonatkoznak.

Az űrtávérzékelés eszközei, termékei

Használatos szenzortípusok

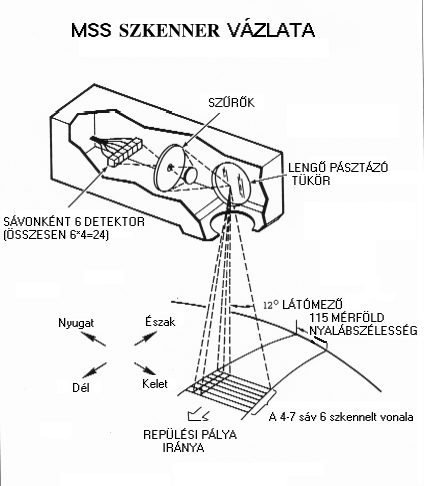
Az első távérzékelési műholdak felbocsátásakor két megoldás között választhattak a tervezők: a képeket elektrooptikai érzékelőkkel készítik és digitális formában a földre sugározzák vagy filmre fényképező automatikus kamarákat alkalmaznak, melyek a leexponált filmeket automatikusan a földre továbbítják. Az első megoldást az amerikaiak választották, a második megoldást a Szovjetunióban alkalmazták.

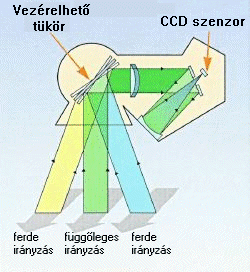
3.55 ábra - a LANDSAT MSS szkenner egyszerűsített vázlat

A szöveg alatti ábra a HVR szenzort vázolja fel. Tekintettel arra, hogy a SPOT szatellitát később konstruálták (1978) érzékelőként már sorszenzorokat alkalmaztak, ezért nem volt szükségük kifejtő tükörre. Az ábrán látható vezérelhető tükör nem is ezt a célt szolgálja, hanem azt, hogy a felvétel függőleges vagy ferde kamara tengellyel készüljön.

A baloldali ábrán a multispektrális ürtávérzékelés veteránjának a LANDSAT műholdak MSS nevű szkannerének vázlatát látjuk. A tipus egyes példányai 1972 és 1992 között működtek a különböző LANDSAT műholdakon. A jelenleg is működő LANDSAT 5 műholdon az MSS-t 1992-ben kikapcsolták.
Amint az ábrából látható a 6 elemből álló szenzorra nem keresztben képezik le a sávot, hanem a repülés irányában. A kereszt irányú leképezést a lengő tükör biztosítaja. Ez más szavakkal azt jelenti, hogy a tükör csatornánként egyszerre 6 vonalról készít digitális felvételt.

3.56 ábra - a francia SPOT műhold HRV nevű szkennere

A digitális megoldás esetén töltéscsatolt félvezető elemekből (CCD) álló egyedi- vagy sor-szenzorokat alkalmaznak ( annyit ahány hullámhossz tartományban érzékelnek egyidejűleg), az egy szenzor(sor)ra történő leképezés geometriája megfelel a fotogrammetriában megismert centrális vetítés törvényszerűségeinek. Az intervallumok szerinti bontást fénybontó prizma és interferencia szűrők segítségével valósítják meg.

A (sor)detektor elemeinek töltését a kiolvasás és analóg-digitális átalakítás után a szatellita rádióhullámok segítségével a földre sugározza. Mivel a vételi körülmények biztosítása az egész pálya mentén nem mindig volt egyszerűen megoldható, a vételmentes területeken az elektronikus képeket magnón tárolják.

A pálya sebessége komoly követelményeket támaszt a kiolvasás és átalakítás sebességével szemben, például a SPOT szatellita esetében a sordetektor két expozíciója közötti idő nem haladhatja meg az 1.5 ms-t.

Míg a képkoordináta rendszer egyik tengelyét a sorszenzor egyértelműen definiálja, a sorok egymásutánját definiáló, a műhold haladási irányába eső másik tengely az idő függvénye. A szatellita pályáján haladva, a föld forgása és kismértékű saját tengely körüli forgása következtében elferdíti a képet s így 700-800 km. magas pálya esetén 20-40 km. hullámhosszú, 40-50 m. amplitúdójú oszcillációk jönnek létre a haladási irányra merőlegesen (a sorok középpontja a haladási irány által meghatározott tengely körül oszcillál). Bár az oszcillációk képeként 20-40 földi illesztőpont felhasználásával jelentősen csökkenthetők, megmaradó részük a felbontás által megengedett legnagyobb nagyításoknál kisebb nagyítást tesz csak lehetővé.

A fényképezés alkalmazása esetén más jellegű problémák adódnak. A szállítható filmanyag korlátozott mennyisége nem teszi lehetővé a hosszabb időn keresztül a folyamatos fényképezést, problémát jelent az exponált negatívok visszajuttatása s jelentős késedelmet okoz, hogy a visszajuttatott negatívokat még ki is kell dolgozni, sőt digitális feldolgozás esetén még a szkennelés is időt vesz igénybe.

Az azonban egyértelmű, hogy a filmfelvételek felbontása, geometriai korrektsége ma még jóval alkalmasabbá teszi őket a sorkamarával készült képeknél a térképészeti-térinformatikai felhasználásra. Ugyanakkor a globális megközelítést igénylő monitoring jellegű feladatok (pld. egy adott évre a világ gabonatermésének előrejelzése) csak automatikus üzemű opto-elektronikus érzékelőkkel ellátott műholdakkal oldhatók meg. Az is világos ugyanakkor, hogy a félvezető technika fejlődése műszakilag lehetővé teszi hogy a keretkamarák a polgári célú műholdakon is alkalmazásra kerüljenek s ezzel a filmen történő távérzékelés előnyei a minimálisra csökkennek.

A nagyfelbontású polgári célú digitális űrtérképező rendszerek létrehozásának napjainkban már nem elsősorban technikai inkább politikai akadályai vannak. 1994 februárjában több amerikai cégből álló konzorcium keresetet nyújtott be az USA Kereskedelmi Minisztériumába, hogy engedélyezze az Eyeglass szatellita projektet. A tervezett szatelliták olyan 1 méter felbontású fekete-fehér digitális képeket készítenének és sugároznának a világszerte elszórt vevőhálózat antennái felé, melyek jó minőségű ortofotó térképek, s általában nagyfelbontású térinformatikai rendszerek alaptérképeinek létrehozására használhatók. A tervezett minőségű felvételeket korábban csak a kém-műholdak részére specifikálták.

Jelenleg (1997 közepe) a projekt ott tart, hogy a minisztérium által 1995-ben kiadott négy engedélyből egy tulajdonosa a Space Imaging EOSAT nevű vállalat 1997 végén kivájna fellőni a jobboldali fényképen bemutatott IKONOS 1 nevű szatellitáját, mely KODAK gyártmányú mátrix szenzora 1 m.-nél jobb felbontást biztosít a fekete fehér (pankromatikus), és 4 méteres felbontást a négycsatornás (vörös, zöld, kék, közel infravörös) multispektrális képek számára. A fénysugarak összegyűjtését könnyű tükrös távcső biztosítja.

A műhold, hasonlóan a SPOT-hoz, tükrök segítségével függőleges és ferde képeket is tud gyűjteni. Míg azonban a SPOT csak a pálya mentén vagy azzal párhuzamosan pásztáz, addig az IKONOS 1 a pályára merőlegesen 130 km * 76 km-es sáv felmérésére is alkalmas. A hivatkozott tartományban magányos képek is exponálhatók, méretük 11 km * 11 km.

Egyszerű geometriai szemléletből belátható, hogy az oldalra néző felvételek felbontása kisebb mint a függőleges felvételeké (a ferdeségi szög koszinuszával el kell osztani a függöleges esetnek megfelelő eredeti földi pixel oldalhosszát) ezért ha az oldalra néző felvételeknél is biztosítani akarjuk az 1 m-es felbontást ez azzal jár, hogy a pályamenti felbontás jobb lesz 1 m.-nél. Az elmondottakat, beleértve a felbontás különbség vizuális hatását jól szemlélteti a 3.58 ábra.

3.58 ábra - a felvételi magasság kapcsolata a széleken való felbontással

3.57 ábra - az IKONOS 1 tesztelés közben

A további engedélyek közül egyet az ORBIMAG vállalat kapta, mely az 1 m-es felbontást az OrbView-3 műholdján kivájna realizálni. Hogy ennek a felbocsátása mikorra várható azt egyelőre nem tudjuk.

A harmadik résztvevő az Earth Watch cég két szatellitára kapott engedélyt melyekkel két lépcsőben kivájna elérni a kitűzött célt.

3.59 ábra - az EarlyBird műhold makettje

3.60 ábra - a QuickBird műhold makettje

Az EarlyBird műhold felbocsájtására a tervek szerint 1997 nyarán kerül sor. A műhold tulajdonképpen átmenetet jelent a méteres felbontás felé, mivel pankromatikus (fekete-fehér) szenzora 3 m felbontású a nadírban. Egy exponálásra 3 km * 3 km-es négyzetet fényképez. Ez a műhold is képes 30 fokos pályairányú és 28 fokos oldalirányú pásztázásra. A multispektrális szenzor (zöld, vörös, közel infravörös) 15 m-es felbontású a nadírban és egy exponálással 15 km * 15 km-es területet fényképez le. Érdemes megemlíteni, hogy a pixeleket 8 bittel írja le szemben az IKONOS 1 11 bitével.

A QuickBird tervezett fellövési idejéről nincs adatunk. A pankromatikus szenzor felbontása 0.82 m nadírban. Egy kép mérete 22 km * 22 km. Ez a műhold is képes sáv térképek készítésére. A multispektrális szenzora (kék, zöld, vörös és közel infravörös) 3.28 m felbontású a nadírban és egy fénykép 22 km * 22 km-t fed le. A pixelek kódolására ez a műhold már 11 bitet használ.

Világméretű hálózat gondoskodik mindkét műhold adatainak vételéről, a vevőállomások vételi körzetén kívül a műholdak rögzítik a felvett információt.

Az EarthWatch cég home page-én egy felméréssel találkozunk, melynek az a célja, hogy felhasználói adatokat gyűjtsön a világ első kereskedelmi radaros műholdja tervezési irányelveihez. Ez a tény is megerősíti azt a meggyőződésemet, hogy a radaros távérzékelés a jövőben még a mainál is fontosabb szerepet fog játszani. Ezért indokolt, hogy nagy vonásokban megismerkedjünk a radaros rendszerek alapelvével.

Radaros távérzékelés

Napjainkban a leggyorsabb fejlődés az aktívan érzékelő radaros rendszerek területén jelentkezik, ezért indokolt e szenzor tipus rövid ismertetése.

A 'RADAR' (RAdio Detection And Ranging) a II. világháború során a repülőgépek felderítésére és távolságuk meghatározására konstruált műszer azon az egyszerű elven működött, hogy mérte azt az időt ami a mikrohullám impulzusok kibocsátása és visszaverődés utáni vétele között eltelik.

A mikrohullámot azért választották, mivel egyenes vonalban terjed, a légköri hatások (pára, felhő, eső) viszonylag kevéssé csillapítják, a hullámhossztól függően viszonylag kis méretű antennákkal jól fókuszálható és a repülőgépek fémes felületéről jól verődik vissza. Amint az alábbiakban látni fogjuk a hullámhossznak a távérzékelési radar rendszerekben is fontos szerepe van, ezért a használt tartományokat a 3.5 táblázatban foglaljuk össze.

Hullámsáv elnevezése	Hullámhossz centiméterben
Ka	0.75 - 1.10
K	1.10 - 1.67
Ku	1.67 - 2.40
X	2.40 - 3.75
C	3.75 - 7.50
S	7.50 - 15
L	15 - 30
P	30 - 100

3.5 táblázat

A távérzékelési radarokat nagy többségükben oldalra néző radar (angol elnevezése Side Looking Airborn Radar, rövidítve SLAR) formájában készítik. A radar antennája a hordozó eszköz pályája irányában helyezkedik el.

3.61 ábra - oldalra néző radar sémája

3.62 ábra - néhány jelölés az oldalra néző radar elvi sémáján

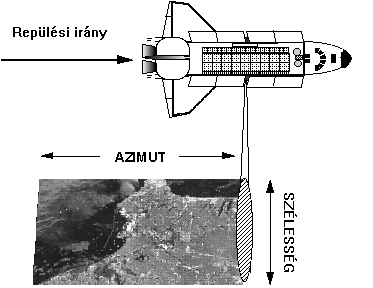
A baloldali ábra (3.61) sematikusan vázolja fel az űrsiklóra szerelt SLAR-t felvételkészítés közben, s bemutatja az elkészült felvétel egy kis részletét is.

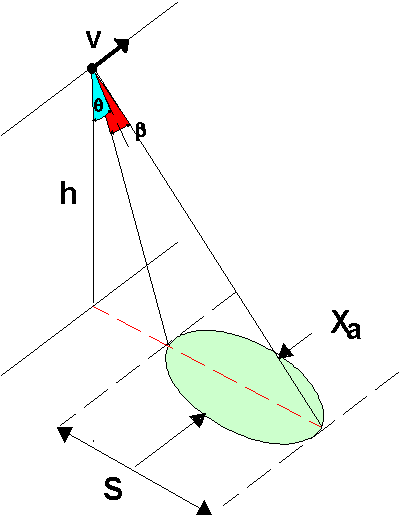
A 3.62 ábrán pedig kiegészítésül feltüntettük azokat a geometriai paramétereket is, melyek az oldalra néző radar felvétel egy sávját jellemzik. A radar egy impulzus kibocsátásakor ellipszist világít meg a földfelszínen, az ellipszis méretei attól függnek, hogy milyen az adott irányban az antenna irányítottsága (fókuszáltsága).

Homogén, pontszerű sugárzó (pld. parabola antenna) esetén az antenna által kibocsátott sugárkúp szöge:

, ahol a hullámhossz, D pedig az antenna átmérője.

Az oldalra néző radarrendszereket azonban úgy igyekeznek kialakítani, hogy a repülési irányban keskenyebb a repülésre merőlegesen pedig szélesebb területeket sugározzanak be. Erre az esetre téglalap alakú antennát feltételezve a megvilágított ellipszis nagy tengelyére (a besugárzott sáv szélességére) a következő közelítő összefüggések írhatók fel:

A képletben a 3.62 ábrán jelölt, illetve a már ismertetetteken kívül alkalmazott jelölések a következők: - a sugárkúp haladási irányra merőleges nyílásszöge, b - a derékszögű antenna haladási irányra merőleges oldalhossza.

Amint már említettük a radar két mennyiséget mér: azt az időt ami az impulzus kibocsájtása és visszaverődés utáni vétele közt eltelik, valamint a visszavert impulzus amplitúdóját, foglalkozzunk röviden először az utóbbival.

3.63 ábra diffúz visszaverődés

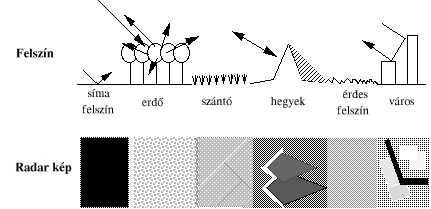
A rádióhullámokból kialakított impulzusok a felszínre érve részben elnyelődnek részben visszaverődnek. A visszavert impulzusok szóródnak és változtatják polaritásukat. Minél egyenletesebb a szóródás annál kisebb a vevőbe jutó 'visszhang' amplitúdója. A diffúz visszaverődés a terep egyenetlenségek és a hullámhossz viszonyának függvénye. Tulajdonképpen csak akkor beszélhetünk diffúz visszaverődésről, ha a terep egyenetlenségek kisebbek a hullámhossz tizedénél.

A vett, visszavert jel amplitúdója tehát többek közt függ:

a jel hullámhosszától, az adó és a vevő polaritásától;
a jel beesési iránya és a terepelem normálisa közti szögtől;
a felszíni egyenetlenségek mérete és a hullámhossz viszonyától;
a felszín elektromos tulajdonságaitól.

3.64 ábra - a különböző terepi objektumok tipikus visszaverődési képei

Ha a vett amplitúdó értékekhez szürkeségi értékeket rendelünk, akkor egy megadott hullámhosszhoz, adó és vevő polaritáshoz illetve oldalszöghöz a 3.64 ábrához hasonló 'jelmagyarázatot' rendelhetünk.

Kézenfekvő, hogyha ugyanarról a területről különböző hullámhosszú felvételeket készítünk, úgy a különböző képek digitális összehasonlításával (lsd. osztályozási eljárások) olyan objektumokat tudunk kiválasztani, melyek megkülönböztetése egy kép esetén nem lehetséges.
Hasonlóképpen az osztályozást segíti, ha ugyanazon a hullámhosszon de különböző adó és vevő polarizációval készítjük a felvételeket. A polarizáció azt jelzi, hogy milyen síkban rezegnek a rádióhullámok; H a vízszintes polarizációt jelöli (tulajdonképpen a rezgés síkját a pálya érintője és az antennából az ellipszis középpontlába húzott egyenes határozzák meg), V pedig az előzőre merőleges síkban rezgő hullámokat jelölő függőleges polarizációt.
Ha a különböző hullámhosszú vagy polaritású képeket vizuálisan szeretnénk értékelni, úgy munkánkat jelentősen megkönnyíti, ha úgy nevezett hamis színes kompozitokat készítünk az egyes képekből.

3.65 ábra - L sáv, vízszíntes adó és vevő polarizáció (LHH)

3.66 ábra - L sáv, vízszíntes adó, függőleges vevő polarizáció (LHV)

3.67 ábra - L sáv, függőleges adó és vevő polarizáció (LVV)

3.68 ábra - L sávú hamisszines kép, HH=kék, HV=zöld, VV=vörös

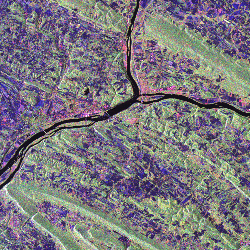
A 3.68 ábrán egy északamerikai helyszín a pensylvaniai SUNBURY hamis színes képét látjuk. A kompozit úgy készült, hogy a HH képhez kék, a HV képhez zöld, a VV képhez pedig vörös színt rendeltek.
A képek szemlélésekor elég nehéz a különbségeket szabad szemmel meghatározni, a színes kép azonban e különbségeket jól érzékelhető markáns színekkel fejezi ki.

A képek szemlélésekor egyelőre nem szabad elfelejtenünk, hogy eddigi ismereteink egyelőre csak egy folt észlelésére vonatkoznak azt még nem tudjuk, hogy miként helyezi el ezeket a foltokat a radarszenzor feldolgozó egysége a radar kép létrehozásakor. Foglalkozzunk tehát a térbeli kifejtéssel.

Mivel egy impulzus a 3.61 és 3.62 ábrákon látható sáv minden pontjáról visszaverődik, s mivel ezek a pontok az antennától különböző távolságra helyezkednek el a visszaverődés után az antenna sok jelet vesz.

Minden vett visszavert impulzus egy pixelt reprezentál a haladásra merőleges sorban, melynek szürkeségi értékét a vett impulzus amplitudója, helyét pedig az impulzus kibocsátása és vétele között eltelt idő határozza meg. Azaz a sávon belüli képalkotás a terjedési időintervallumok sorba állításával, számítással oldható meg.

Két egymástól d_haránt távolságra elhelyezkedő szomszédos pixel reflektált jeleinek időkülönbsége

ahol c a hullám terjedési sebessége. A rendszer haladási értelemre merőleges felbontóképességét a legkisebb detektálható érték határozza meg. Ez az érték megegyezik a kibocsátott impulzus időtartamával -al, azaz a keresztirányú felbontóképesség:

Igy már érthető, hogy miért alkalmaznak oldalra néző megoldást, hisz ha a radar a hordozó objektum alá irányulna helyzet állna elő és a pixelek sávmenti elhelyezése határozatlanná válna.

Ha például és , úgy a felbontás d_haránt = 440 m. A felbontás finomítását az impulzus hossz csökkentésével érhetnénk el, ennek azonban műszaki és energetikai akadályai vannak. A megoldást frekvencia modulált impulzusok kibocsátása nyújtja. Ebben az esetben ugyanis a felbontás független az impulzus hosszától és csak SZ-től a frekvenciamodulált jel sávszélességétől függ az alábbiak szerint:

A frekvencia moduláció előnyeit jól szemlélteti, hogy SZ = 20 MHz sávszélesség és oldalszög esetén változatlan impulzus hossz mellett a felbontóképesség d_haránt = 22 m.-re rövidül. Érdekességként megemlítjük, hogy folyamatos frekvenciamodulált jelek visszaverődését már régóta használják repülőgépek magasságának meghatározására [5].

A pálya irányába (azimut irányba) eső felbontást a 3.62 ábrán X_a -val jelölt kistengely jelenti. Felírható, hogy

A képletben jelöli a sugárkúp pálya irányú csúcsszögét, h a repülési magasságot, a pedig az antenna pálya irányú (hossz-) méretét.

Ha példaként reális értékekkel számolunk, úgy a pálya irányú felbontásra d_azimut = 16.3 km. számértéket kapunk. Látható, hogy legfeljebb csak repülőgépre telepített berendezés esetén vehet fel olyan értéket, mely összhangban van a keresztirányú felbontással (h = 1 km. esetén d_azimut = 20.4 m.).

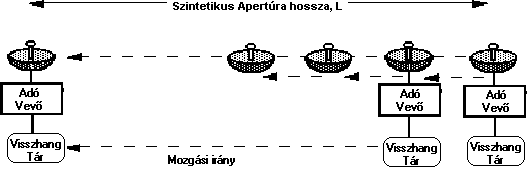
Hogy a pályairányú felbontást reális antennaméretekkel is a keresztirányú felbontás szintjére lehessen hozni a radarfelvételeket az úgy nevezett Szintetikus Apertúrájú Radarok (SAR) segítségével hajtják végre. A SAR alapelvét 1950-ben katonai felhasználásra dolgozták ki, a 60-as években repülőgépre szerelve először alkalmazták polgári célokra (geológiai térképezés), majd 1978-ban először lőttek ki SAR-al felszerelt mesterséges holdat a SEASAT-ot.

A SAR alapelve azon nyugszik, hogy az adó antenna ismert (lehetőleg egyenes) pályán haladva sorra bocsátja ki az impulzusokat. Ha vétel során gondoskodunk arról, hogy ne csak a visszavert impulzusok feszültségét de a fázisukat is (hogy melyik adóimpulzusból származnak) rögzítsük, úgy olyan adatsort nyerünk, mely megfelelő számítógépes feldolgozás után hasonlóan finom pályamenti felbontást ad mintha az antennát a pálya irányában jelentősen meghosszabbítottuk volna.

3.69 ábra - a SAR működési elve

A szemléletesség kedvéért szokták a SAR nyers mérési eredményeit a végleges kép digitális hologramjának is nevezni, melyből a digitális korrelátor csak bonyolult számítások elvégzése után képes a tulajdonképpeni képet előállítani.

A szintetikus apertúrát használó rendszer pálya irányú felbontása várakozásunkkal ellentétben annál nagyobb minél kisebb a valódi antenna pálya irányú mérete, a felbontást jellemző pixelméretet elméletileg az alábbi egyenlőtlenségből határozzák meg:

Gyakorlatilag az elméleti pixel méretnél nagyobb méretek adódnak, igy a példánkban szereplő a = 12 m.-es antenna esetén konstrukciótól függően a pixel pálya irányú szélessége 10 - 20 méter között változhat.

Az vevő és adó antennák általában síkpolarizált hullámokat bocsátanak ki illetve ilyen hullámokat vesznek. Ha a SAR rendszerben mind az adásra mind a vételre rendelkezünk vertikálisan és horizontálisan polarizált antennákkal, úgy nem csak azt tanulmányozhatjuk, hogy milyen reflexiókat szenved a horizontálisan (vertikálisan) polarizált impulzus azonos polarizáltságú vétel esetén, de azt is, hogy hogyan változtatja meg a visszaverődés a hullám polarizáltságát. A visszaverődés során nem csak az intenzitás, polarizáltság de az erőtér fázisa is megváltozik. A visszavert hullám elektromos terét az alábbi kifejezéssel írhatjuk le:

ahol

a visszavert hullám,

a beeső hullám elektromos tere,

a szórási mátrix (a p index az adó antenna, a q index a vevő antenna

polarizációját jelüli), R a visszaverő felület és az antenna távolsága, k_o a megvilágító hullám hullámszáma. A képet vagy az S_pq szórásmátrix meglévő elemeiből építjük fel, ha a komplex visszaverési tényezőt kívánjuk reprezentálni, vagy a értékekből, ha a képet az intenzitás keresztszelvényre alapozzuk. Az elemi intenzitások a szórási mátrix elemek abszolút értékei négyzeteivel arányosak az alábbiak szerint:

Gyakran használják a normalizált keresztszelvényt melynek elemei:

Érdemes megemlíteni, hogy d_haránt tulajdonképpen levezetett mennyiség, mivel a radar a ferde távolságok mentén alakítja ki pixeleit, azaz

ahol a kérdéses pixelre vonatkozó beesési szög.

A radar felvételek rohamos elterjedése az utóbbi néhány évre tehető. Napjainkban már olyan SAR eszközökkel is találkozunk, melyek egyidejűleg több hullámsávon is letapogatják a felszínt. A multispektrális radar felvételek hasznosítására már sok módszert dolgoztak ki, azonban egyelőre még nem rendelkezünk olyan kiforrott eljárásokkal mint a CCD szenzoros multispektrális távérzékelésben. A jelen stádiumban a legfontosabb eredmény, hogy az elméleti megalapozás után megkezdték a radarfelvételek rádiómetrikus korrekcióinak gyakorlati alkalmazását, amiről a következő alpontban szólunk. Már itt fontosnak tartjuk azonban megjegyezni, hogy minden radar kép felhasználásakor tudnunk kell, hogy a kérdéses képet ellátták-e rádiómetrikus korrekcióval vagy sem.

A radar képek sajátosságai között meg kell említenünk azokat a problémákat, melyeket a ferde felvételi mód okoz. Arról, hogy a kép tulajdonképpen ferde síkokban képződik már szóltunk, azonban meg kell említenünk, hogy e miatt minden pixelt geometriai korrekcióként le kell vetíteni a felületre. Kevéssé kezelhetőbb probléma, hogy a felszín domborulatai leárnyékolják a mögöttük lévő részeket. Ez a probléma azonban rendszerint csak alacsonyabb repülési magasságok illetve magas hegyek esetén lép fel.

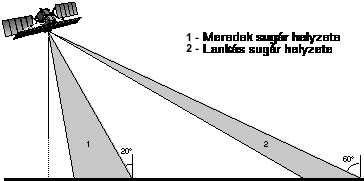
3.70 ábra - a RADARSAT kéthajlású SAR műszere

A keresztirányú felbontás vizsgálatakor láttuk, hogy minél inkább eltér a függőlegestől a radar irányítottsága annál finomabb a felbontás. Az előbb viszont arról is szóltunk, hogy erős domborzatú terepen a sugár ferdeség növekedésével nő a hasznos információ leárnyékolása. A kettős problémán úgy próbál segíteni a RADARSAT nevű kanadai műhold SAR műszere, hogy az antenna két dőlési értékre állítható.

A 3.70-es ábrán látható 1-es sugárhelyzetet dombos - hegyes vidékeken alkalmazzák, míg a 2-es helyzetű sugárral a sík területeket pásztázzák.

A szintetikus apertúra megvalósításához az szükséges, hogy a koherens hullámokat szuperponálják e közben azonban olyan interferencia jellegű hatások léphetnek fel melyek pöttyössé teszik a képet. Ezt a hatást nevezik 'speckle effektusnak'. Csökkentésére átlagoló szűrőt alkalmaznak az intenzitás alapú képen.

A rádiómetrikus korrekció fogalma

Bármilyen szenzort is alkalmazzunk a célunk az, hogy olyan számértékeket kapjunk a földfelszín minden felületelemére (a felületelem vagy pixel konkrét méretét a rendszer felbontása határozza meg), mely megadja az adott területet borító (illetve alkotó) természetes és mesterséges objektumok átlagos reflexiós (visszaverési) együtthatóját egy megadott hullámhosszra vagy hullámsávra. Az átlagos jelzőre azért van szükségünk, mivel a felületet nem feltétlenül homogén objektumok borítják illetve alkotják.

A felszínről visszaverődő sugárzás az atmoszférán át jut a szenzor objektívjére, majd különböző bonyolult optikai elemeken keresztül gerjeszt töltést a CCD sorszenzor elemeiben. A szenzor akkor működik jól, ha valamennyi CCD elem valamennyi hullámhossz intervallumban azonos energia hatására azonos töltésszintet (potenciált) hoz létre.

Bár első közelítésként a belépő energia és a potenciál között lineáris kapcsolat áll fenn, a gyakorlatban ez a kapcsolat eltérhet a lineáristól és cellánként is különböző lehet. A radiometrikus korrekció első feladata a fentiek szerint az, hogy a CCD elemek potenciál válaszát a fényenergiára azonos szintre hozza.

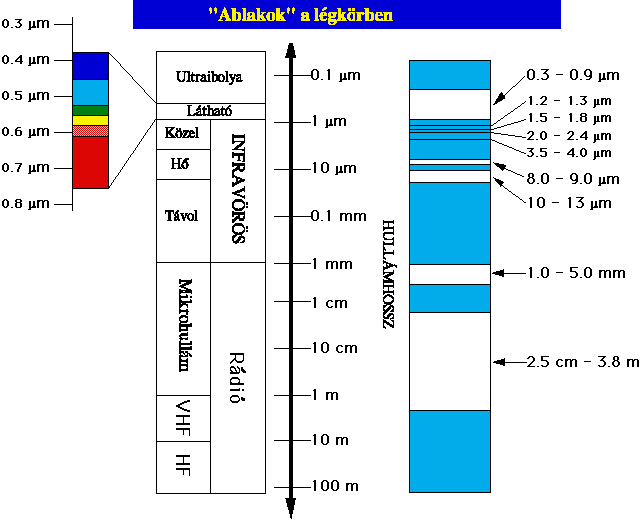
A további javítás részek közül csak kettőre szeretnék utalni. A sáv detektor szélére leképezett pixelek messzebb vannak a CCD elemektől mint középre leképezett társaik ezért az atmoszféra csillapító hatása következtében azonos visszavert energia esetén is gyöngébb potenciált hoznak létre, ezt a szabályos hatást is figyelembe kell venni a kalibráláskor. Az atmoszférát alkotó gázok és gőzök csillapítása a földfelszínről visszaverődő sugárzásra függ a kérdéses hullám hosszától. Bár általánosan azt mondhatjuk hogy az elnyelés a hullámhossz növekedésével csökken ez a kijelentés csak akkor igaz, ha figyelembe vesszük hogy míg a látható fény csillapítása alapvetően az atmoszféra legapróbb víz- és füstrészecskéin (aerosol) előálló szóródás következtében jön létre, addig az infravörös tartományban a csillapítást döntően az atmoszférát alkotó gázok és gőzök molekuláris elnyelése okozza. Az általános szabály az infravörös tartományra tehát csak akkor érvényes, ha a méréseket az elnyelési sávok közötti ablakokban végezzük. A légköri ablakokat a 3.71 ábrán vázoltuk fel. A már hivatkozott tankönyvben [5] részletesebb grafikonokat is találhat az érdeklődő.

3.71 ábra - áteresztési ablakok a légkörben

A radar szenzorok radiometrikus kalibrálása viszonylag új téma. A kalibrálást elvégezhetik a műszer különböző blokkjainak mérésével, ezt az úgy nevezett belső kalibrálást azonban célszerű terepi kalibrálással megerősíteni. Anélkül, hogy túlságosan belemennénk a részletekbe szeretnénk felhívni az olvasó figyelmét a kalibrálás néhány fontosabb csomópontjára (a részletek iránt érdeklődőknek Freeman előadását [13] ajánljuk a figyelmébe).

Talán a legfontosabb kalibrálási csomópont az adó és vevő antennák nyereségének meghatározása. A nyereségi értékek határozzák meg ugyanis, hogy azonos jel erősségből az antenna mennyit sugároz ki adott irányba, illetve mennyit vesz adott irányból. Ezek az értékek tehát függnek a felszínre vetített képelem középpontját az adó illetve vevő antennával összekötő térbeli egyenes helyzetétől. Bár ezt a vizsgálatot földi körülmények között is el lehet végezni. a tapasztalat azt bizonyítja, hogy a zord repülési körülmények között a radar antennák karakterisztikái megváltozhatnak, ezért azok repülési körülmények közötti kalibrálására is szükség lehet. A tereppontot az antennával összekötő egyenes térbeli helyzete a hordozóeszköz illetve az antennák koordináta rendszerében azonban függ a hordozó eszköz elfordulásaitól is melyeket ezért valamilyen elfordulás mutató műszerrel regisztrálni kell. Kalibrálni kell az erősítést, a csillapításokat a késleltetéseket (beleértve az atmoszféra hatását is a hullám törésmutatójára) valamint figyelembe kell venni a földgörbület hatását is ahhoz, hogy a radarképen a pixel távolsága és intenzitása megfeleljen valóságos helyének és a hely visszaverő képességének.

Külön figyelmet érdemel a különféle zajok hatásának vizsgálata, amikor is a méréseket kikapcsolt adóantennával hajtják végre s így a processzorból kilépő jel, mely kizárólag a zajok következménye, figyelembe vehető.

Igen nagy a jelentősége a processzor kalibrálásának, melyet szimulált szabványos jelek segítségével hajtanak végre.

Az elmondottak érzékeltetik, hogy mennyire bonyolult mérőrendszerről van szó, melyben az egyes csomópontokon elkövetett kalibrálási hibák lényegesen megváltoztathatják a végterméket. Ez az oka annak, hogy a belső kalibrálást rendszerint terepi kalibrálással is ellenőrzik. A terepi kalibrálás azt a célt is szolgálhatja, hogy segítségével eldöntsük vajon valamely szenzor által előállított radarkép kalibrált-e vagy sem.

A külső kalibrálás céljaira olyan területet keresünk, mely reflexiós tényezője az adott hullámsáv, polaritás, geometria szempontjából ismert és homogénnak vehető. A gyakorlatban mezőgazdasági művelés alatt álló táblákat, tropikus erdőket és északi erdőket szoktak választani. Az eljárás során átlagolják a képekben mért pixel teljesítményeket a természetes pötty-hatás csökkentése érdekében, és a becsült átlagos hiba értékét kivonják az átlagból. A mért és az ismert visszaverődési értékek birtokában a kalibrációs függvény számítható.

Távérzékelés I