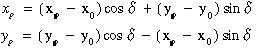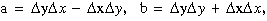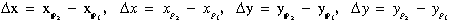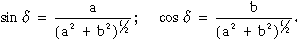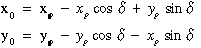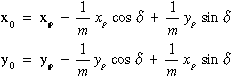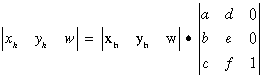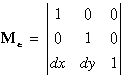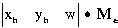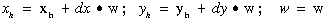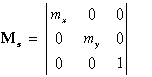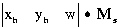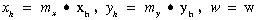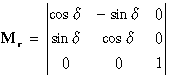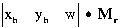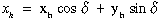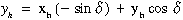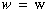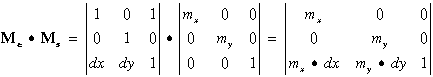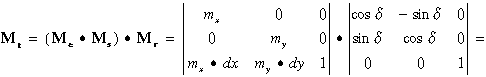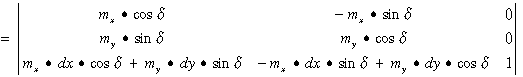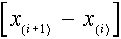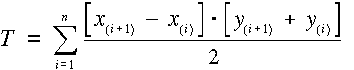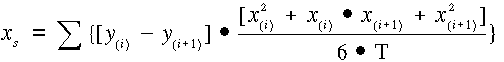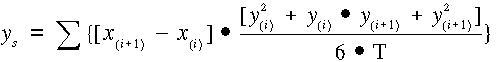Alapműveletek vektoros és raszteres térbeli adatokkal II

Ebben a részben a vektoros adatokkal végezhető számítások közül megismerkedünk:

a síkbeli transzformációkkal,
a távolság fogalmakkal,
az egyenes szakaszok metszéspontjainak megkeresésével,
a hossz-, terület-, kerület-, súlypont számításokkal,
a pont a poligonban algoritmussal.

Síkbeli transzformációk

A térbeli objektumok helyzetét úgy tudjuk a legkényelmesebben figyelembe venni, ha valamilyen, derékszögű vagy görbe vonalú, alapnak elfogadott, koordináta rendszerben rögzítjük jellemző pontjaik koordinátáit. Az alapként elfogadott koordináta rendszerekről, az úgy nevezett referencia rendszerekről, még részletesen szólunk. Egyelőre elég annyit figyelembe vennünk, hogy bár e rendszereket csak két csoportra osztják abszolút és relatív (a Föld olyan fizikai tulajdonságaival meghatározott mint a tömegközéppont és a forgástengely, illetve önkényesen a Földhöz rögzített), mégis mindkét csoportnak a gyakorlatban sokféle realizálását használják. Ezek a koordináta rendszerek térbeliek. A gyakorlati térképezés igényeiből kiindulva azonban ma még az esetek túlnyomó többségében nem a pontok térbeli koordinátáit használják, hanem azok vetületeit valamely célszerűen felvett síkra vagy síkba fejthető felületre (henger, kúp). E vetületekből gyakorlatilag végtelen sokkal találkozunk. Ha a vetítés során a harmadik komponenst a magasságot is meghatározzuk úgy azt a térinformatikai rendszerek szinte kizárólag mint attributív adatot kezelik. Ha ezen kívül még arra is gondolunk, hogy a különböző referencia rendszerekből különböző módszerekkel különböző elhelyezkedésű síkokra vetített térképek elvileg végtelen sok méretarányban készülhetnek, úgy feltehetőleg igazolt az az elképzelésünk, hogy a transzformációknak sulyponti szerepük van a térinformatikai rendszerek alapműveletei között.

Meg kell még indokolnunk, hogy miért foglalkozunk e helyen csak a síkbeli transzformációkkal. Ennek legfőbb oka, amint már utaltunk rá, hogy a kereskedelmi GIS és LIS rendszerek tulajdonképpen kétdimenziós rendszerek, bár egyesek közülük a magasságok felhasználásával térbeli ábrázolásra is alkalmasak. A 3D-s megjelenítéshez tartozó transzformációkról a vizualizálási műveletekkel kapcsolatban fogunk szólni. A valódi térbeli transzformációkról pedig a referencia rendszerrel és a fotogrammetriai és GPS adatnyeréssel kapcsolatban közlünk rövid összefoglalást. Didaktikai szempontból is szerencsésnek tartjuk, hogy egy nem matematikai könyvben az egzaktabb fogalmak bevezetését egyszerűbb formájukban végezzük.

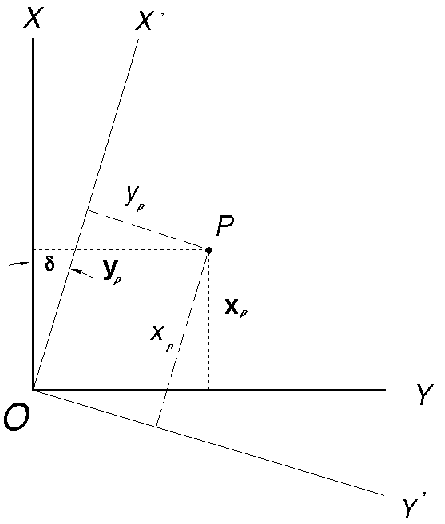
A sík transzformáció legegyszerűbb esete ha pontjainkat olyan koordináta rendszerbe akarjuk átszámítani, mely kezdőpontja nem esik egybe az eredeti koordináta rendszer kezdőpontjával, X tengelye pedig szöget zár be az eredeti koordináta rendszer X tengelyével (2.38 ábra).


2.38 ábra - eltolás és elforgatás a síkban
Az átszámított koordináták az új rendszerben:
ha és akkor:
A második koordinátarendszer kezdőpontjának első rendszerbeli koordinátái:

A transzformációs paraméterek tehát kiszámíthatóak, ha ismerjük két pont koordinátáit mind a két rendszerben. A valóságban azonban a két rendszer között rendszerint méretarány különbség is van gondoljunk csak arra, hogy a helyi vízszintes ipartelepi geodéziai hálózatokat nem redukálják a tengerszintre és gyakran vetületi korrekciókkal sem látják el ez pedig azt eredményezi, hogy a két hálózatban a méter más és más fizikai hossznak felel meg. A két pont (P₁, P₂ ) két rendszerbeli koordinátáiból (x_P1,y_{P 1}, x_P2,y_{P 2}), (x_P1,y_{P 1}, x_P2,y_{P 2}) a méretarány tényezőt egyszerűen kiszámíthatjuk hisz

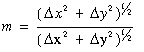
azaz m a két pont kétféle koordinátarendszerben kiszámítható távolságának hányadosával egyenlő. Érdemes megjegyezni, hogy a számlálóba az a koordináta rendszer kerül (esetünkben a dültbetűs), amelybe az átszámítást végezzük.

A transzformációs képletek a méretarány tényező figyelembe vételével a következő alakot nyerik:

Az elfordulást kifejező sin és cos számítására a méretarány tényező nincs befolyással

A második (dűlt betűs) koordináta rendszer kezdőpontjának első rendszerbeli koordinátái pedig a következőképpen alakulnak:

A gyakorlatban a transzformáció végrehajtásához kettőnél több mindkét rendszerben ismert koordinátájú pont koordinátáit vesszük igénybe. Ezt a feladatot HELMERT féle hasonlósági transzformációnak hívják. A transzformációt azért nevezik hasonlóságinak, mivel nem változtatja meg a transzformált pontok által képzett idomok alakját. A feladat legkisebb négyzetek módszere szerinti megoldása az alábbi egyszerű képletekre vezethető vissza.

Legyen:

akkor a keresett síkkoordináták a második rendszerben:

Különösen fényképeken ábrázolt objektumok reális alakjának helyreállítására gyakran alkalmaznak affin transzformációt. Ennél a transzformációnál hat különböző paraméter figyelembevételére van szükség, azaz legalább három pont mindkét rendszerbeli koordinátáit kell ismernünk a paraméterek meghatározásához.

Korábbi jelöléseinket megtartva (az ismeretlen együtthatókat kis dűlt betűkkel jelölve) a transzformációs egyenletek az alábbiak:

Affin transzformációt eredményez az a speciális eset is amikor a két koordináta tengely irányában különböző méretarány tényezőt indokolt alkalmazni. Ilyen eset állhat elő akkor, ha a térképlapok helytelen tárolása következtében a két főirányban különböző zsugorodások jönnek létre.

Szinte valamennyi kereskedelmi GIS szoftver ismeri az u.n. gumilepedő transzformációt. A transzformációt szakszerűbben polinomos transzformációnak nevezhetjük, mivel a két koordináta rendszer között két n-edfokú polinom teremti meg a kapcsolatot az alábbiak szerint:

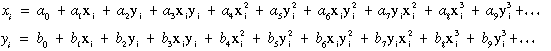
A polinomok együtthatóinak meghatározásához esetünkben tíz pont mindkét rendszerbeli koordinátáit kell ismerni. A gyakorlatban rendszerint megelégednek a másodfokú közelítéssel, harmadfokúnál magasabb fokszámú polinomot pedig szinte soha sem használnak, ugyanis azt tapasztalták, hogy a magasabb fokszámú polinomok, bár figyelembe veszik a helyi torzulásokat, a két koordináta rendszer globális elhelyezkedésére nem nyújtanak megnyugtatóbb választ.

A síkbeli (és térbeli) transzformációk iránt érdeklődő olvasóinknak ajánljuk Wolf [11] és Detrekői [12] kiegyenlítő számításokat tárgyaló összefoglaló munkáit.

Bár a transzformáció lényegén mit sem változtat, hogy mire használjuk, a gyakorlat mégis úgy hozta, hogy a geodéziai transzformációk eszköztárukban is különböznek a számítógépes grafika által használt transzformációs módszerektől. Ez a jelenség mindenek előtt azzal magyarázható hogy a geodéziában a pontok rögzítettek és a koordináta rendszereket transzformálják, tehát azok tolódnak el, forognak és zsugorodnak. A kompjuter grafikában fordított a helyzet: a rögzített képernyő koordináta rendszerhez képest a pontok mozognak és e mozgásoknak megfelelő új helyet jellemző koordináták a transzformáció eredményei. Ez a különbség megfelelő előjel konvenciókkal ugyan a korábbi módszerekkel is figyelembe vehető lenne, mégis érthető az új módszerek megjelenése, ha arra gondolunk, hogy a kompjuter grafikában a szemléletesség érdekében nagy tömegben végzik a transzformációkat, s ezek megfogalmazását igyekeznek maximálisan leegyszerűsíteni, másrészt ezek a módszerek csak a közelmúltban alakultak ki, s a hosszabb időre visszatekintő geodéziai és fotogrammetriai transzformációk, kialakulásuk idején, még nem használhatták őket.

A transzformációk leegyszerűsítését a homogén koordináták bevezetése tette lehetővé. E koordináták bevezetésével minden transzformáció önálló matematikai egységként kezelhető, s egyben biztosítható az egymás után következő transzformációk összekapcsolása (konkatenálása).

A módszer lényege, hogy a síkbeli pontokat két koordináta helyett három koordinátával azonosítjuk, azaz valamely P pont [x, y] koordináta párosa helyett a [x_k, y_k, w] koordináta hármast használjuk. Az eredeti koordináták a homogén koordinátákból az alábbi egyszerű kifejezésekből számíthatók:

Matematikailag a homogén koordináták alkalmazása azt jelenti, hogy az n dimenziós térből áttérünk az n+1 dimenziós térbe, ahol az n dimenziós pontok úgy tekinthetők mint az n+1 dimenziós tér alterei.

A leképezés az n dimenziós térből az n+1 dimenziós térbe többértékű, azaz az n dimenziós térbeli alakzat végtelen sok formulával adható meg az n+1 dimenziós térben. E leképezés inverze a projekció, ez az n+1 dimenziós tér pontjait képezi le az n dimenziós térbe.

Ha a gyakorlati oldalról próbáljuk megközelíteni a kérdést, úgy egyszerűen azt mondhatjuk, hogy a homogén koordináták bevezetése a mátrix algebra szabályai alapján lehetővé teszi, hogy minden transzformáció az eredeti homogén koordinátákból álló vektor és egy transzformációs mátrix szorzataként álljon elő (azaz a homogén koordináták az eredeti koordináták egy olyan azonos átalakításának eredményei, melyek ezt az egyszerű transzformációs műveleti szabályt lehetővé teszik).

Általános esetben a transzformációt a következő kifejezéssel írhatjuk le:

Ha a 3x3-as transzformációs mátrixot a továbbiakban M_i-vel jelöljük, ahol i a transzformáció milyenségére utaló index (i=e - eltolás, i=s - skálázás, i=r - forgatás), úgy az egyes rész transzformációkra a következő kifejezéseket kapjuk:

eltolás esetén

eredménye:

skálázás (méretarány változtatás) esetén

eredménye pedig:

a kezdőpont körüli, az óramutató járásával megegyező pontelfordulás esetén, matematikai koordináta rendszerben

eredménye pedig:

Szeretnénk a szövegben is felhívni arra a figyelmet, hogy matematikai koordináta rendszerben dolgozunk azaz a 2.38 ábrán látható geodéziai koordináta rendszer X és Y koordináta tengelyei helyet cserélnek, és nem a koordináta tengely forog a ponthoz képest, hanem fordítva.

Az a tény, hogy w értéke az eddigi transzformációk során nem változott azt jelenti, hogy a transzformáció eredménye az eredeti altérben marad. A gyakorlatban w = 1 értékkel szokták a számításokat végezni. Ha mi is elfogadjuk ezt az egyszerűsítő konvenciót, és azt az általános esetet keressük, amely eltolás, skálázás és forgatás együttes alkalmazásával mozgatja a pontot, akkor az eredő transzformációs mátrixot a komponens mátrixok összeszorzásával nyerjük az alábbiak szerint:

A transzformált pontkoordináta vektor pedig mint a transzponált transzformációs mátrix és az eredeti koordináta vektor szorzata nyerhető:

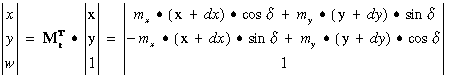
Az ismertetett síkbeli transzformációk állandó velejárói az összetettebb GIS műveletek végrehajtásának. Ugyanezen műveletek térbeli megfelelői viszont sokkal kevesebb térinformatikai szoftverben kerülnek alkalmazásra. Ezért tartjuk indokoltnak, hogy a térbeli transzformációkkal csak azután foglalkozzunk miután megismerkedtünk a 3 és 2.5 dimenziós adatmodell fogalmával, mely modellekben összefoglalt adatok manipulálására és megjelenítésére ezek a transzformációk felhasználhatók.

Távolságfogalmak

Vektoros adatmodell alkalmazása esetén megszokott szemléletünkhöz legközelebb az Euklides-i távolság fogalom áll, mely két, egy síkban fekvő pont távolságát a Pythagoras tétel segítségével definiálja:

azaz a két pont közötti távolság a két pontot összekötő egyenes hosszával egyenlő.

Számunkra szokatlan, de a térinformatikában gyakran használt távolság fogalom u.n. Manhattan vagy háztömb távolság, mely meghatározás szerint

azaz a háztömb távolság nem más, mint a két pont koordinátakülönbségei abszolút értékeinek összege. E távolság fogalom keletkezésével (amint elnevezése is mutatja) az amerikai városok derékszögű utcahálózatához kötődik, hisz reálisabban tükrözi az Euklides-i távolságnál a két különböző utcán található pont közötti valódi távolságot. Különösen használatos e fogalom a raszter grafikában, ahol két pixel közötti diszkrét távolság, pixelekben kifejezve, másképpen nem is adható meg.

Egyenes darabok metszéspontjai

Az egyenes darabok metszéspontjainak meghatározása szinte valamennyi FIR művelet alapját képezi vektoros adatmodell esetén, ezért a feladat egyszerű volta ellenére is megérdemli, hogy röviden összefoglaljuk. A térinformatikai feladatokban az egyenesek általában végpontjaikkal kerülnek megadásra. Ha az első egyenes kezdő illetve végpontjának koordinátái (x₁, y₁), (x₂, y₂), a másodiké pedig (u₁, v₁), (u₂, v₂), akkor a két egyenes iránytangenseire, tisztatagjaira és metszéspontjaira a következő értékeket kapjuk:

A jobboldali kifejezés azonban csak a két - két pont által meghatározott végtelen hosszú egyenesek metszéspontját szolgáltatja, mely nem feltétlenül van rajta a figyelembe veendő szakaszokon. Azt, hogy a pont valóban rajta van e az első egyenes szakaszon a

feltétel teljesülése tanúsítja. Hasonlóképpen, a

feltétel teljesülése arról tanúskodik, hogy a metszéspont a második egyenes szakaszon is rajta van. Mivel bármelyik egyenes függőleges is lehet, amikor is x₁=x₂=x_i vagy u₁=u₂=u_i a feltételeket az y koordinátákra is meg kell vizsgálni.

A fenti képletek programozásakor figyelembe kell venni, hogy ha valamelyik egyenes függőleges az iránytangens egyenletek egyike a zérussal való osztás következtében hibát jelez. Hasonló hiba jelentkezik párhuzamos egyenesek esetén az x_i számításakor.

E hibák megkerülhetők, ha függőleges egyenes esetén (x₁=x₂ , vagy u₁=u₂ ) a metszéspont koordinátáját egyenlővé tesszük a függőleges egyenes x koordinátájával (x_i=x₁ , vagy x_i=u₁), és ezt az értéket a nem függőleges egyenes egyenletébe behelyettesítve nyerjük a metszéspont y koordinátáját. Párhuzamos egyenesek esetén azaz, ha b₁=b₂ véges metszéspont hiányában a programot leállítjuk.

A térinformatikai feladatokban rendszerint nem két izolált egyenes metszéspontjára van szükségünk, hanem egyenes szakaszokból álló vonalak metszéspontjait keressük. Ezek a vonalak gyakran zártak, az így létrejövő zárt sokszögeket a térinformatikai irodalom az angol szaknyelvből átvéve poligonoknak nevezi. A térinformatikai szoftver funkciók kapcsán bemutatandó fedvényezési művelet nagytömegű metszéspont számítást igényel összetett vonalak illetve poligonok között. Ezért indokolt röviden megnézni, hogy miként alkalmazhatók a metszési képletek sok egyenes szakaszból álló összetett vonalak metszéspont számításaikor.

Az egyszerűség kedvéért tételezzük fel, hogy két összetett vonalunk van, az egyik n₁, a másik n₂ egyenes szakaszból áll. Ha mechanikusan alkalmazzuk erre az esetre a két egyenes szakasz metszéspont meghatározására ismertetett összefüggéseinket, úgy csak annyit kell tennünk, hogy két ciklusba foglaljuk a képleteket, a külső ciklus pld. az első vonal szakaszai szerint változhat, míg a belső ciklus a második vonal szakaszai szerint. Az így felépített program sorra veszi az első vonal szakaszait, tehát először az első szakaszt, és megnézi ennek a szakasznak a metszéseit a második vonal összes szakaszával. Az igy kialakított program műveletigénye tehát arányos az n₁*n₂ szorzattal (a számítástechnikai irodalom ezt a tényt az o(n₁*n₂ )kifejezéssel jelöli).

Mivel, amint már említettük, a gyakorlati feladatokban a számítandó metszések száma igen nagy, ezért a használhatóság érdekében a térinformatikai szoftverek különböző trükköket alkalmaznak az elvégzendő számítások csökkentésére. Bár e trükkök alkalmazása újabb műveletek beiktatását igényli a programba, alkalmazásukkal elérhető, hogy a műveletigény nagyságrendje megközelítse az o(n₁+n₂) értéket.

E trükkök közül talán legszemléletesebb a befoglaló téglalapok módszere. Mindkét összetett vonalat egy egy téglalappal veszünk körül, melyek sarokponti koordinátái (x₁_min, y₁_min ), (x₁_min, y₁_max), (x₁_max, y₁_max ), (x₁_max, y₁_min), illetve (x₂_min, y₂_min), (x₂_min, y₂_max), (x₂_max, y₂_max), (x₂_max, y₂_min), és megvizsgáljuk, hogy a két befoglaló téglalap fedi-e egymást. A vizsgálat igen egyszerűen négy egyenlőtlenség kiértékelését igényli:

2.39 ábra - a befoglaló téglalpok módszere

Ellenkező esetben a két vonalnak nincs metszéspontja. Ha a két téglalap fedésben van, úgy el kell készíteni mindkét vonal valamennyi szakaszának befoglaló téglalapjait, és a fönti eljárással ki kell választani azokat, melyek fedik egymást. A metszések számításába csak a kérdéses vonalszakaszokat kell bevonni.

	(a 2. téglalap az 1. téglalap fölött van)
	(a 2. téglalap az 1. téglalap alatt van)
	(a 2. téglalap az 1. téglalaptól jobbra van)
	(a 2. téglalap az 1. téglalaptól balra van)
Ha a fenti egyenlőtlenségek közül valamelyik nem teljesül, úgy a két téglalap fedésben van, tehát valószínű, hogy a két összetett vonalnak van(nak) metszéspontja(i).

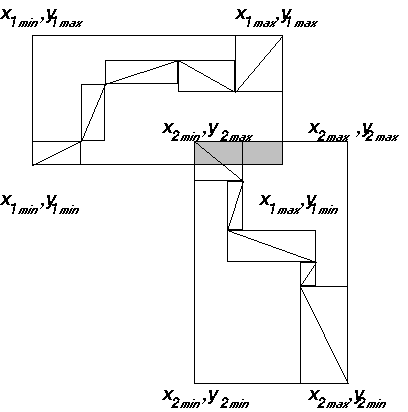
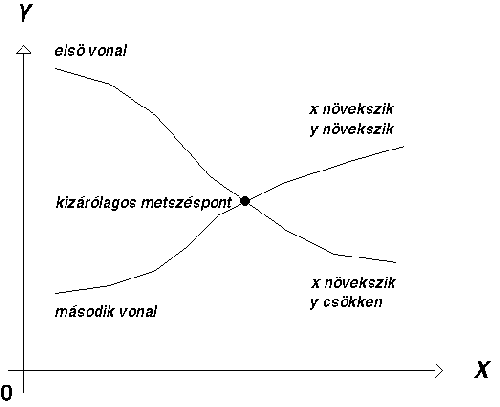
A metszéspont keresésre fordított gépidő jelentősen csökkenthető az összetett vonalak monoton szakaszokra bontásával is.

2.40 ábra - a monoton szakaszokra bontás módszere

Ezután már csak azt kell megkeresni, hogy a két monoton szakasz melyik két összetevő egyenes darabja metsződik. Elvileg alkalmazhatnánk az általános algoritmust (az első vonal minden egyes szakaszának metszését a második vonal minden egyes szakaszával) azzal a különbséggel, hogy az első metszéspont megtalálása után (mivel több nem lehet) leállítjuk a keresést. Tovább csökkenthető a számítási munka, ha a megfelelő monoton szakaszokat x szerinti intevallumokba rendezzük, és összehasonlítjuk a két görbe azonos x intevallumaihoz tartozó átlagos y értékeket. Ahhoz az intervallumhoz tartozó egyenesszakaszok metszés számításait kell csak elvégezni, melynél a két görbe átlagos y értéke közel megegyezik.

A monotonitás azt jelenti, hogy x monoton növekedésével az adott vonalszakaszon y monoton növekszik vagy csökken. A monoton szakaszokat az x vagy y tengellyel párhuzamos egyenesek csak egyszer metszik. Ha két monoton szakasz közül az egyik y-ban növekvő, a másik peddig csökkenő, és van már egy metszéspontjuk, úgy több metszéspontjuk már nincs.

Hossz-kerület, terület és súlypont számítások

Vektoros adatmodellben a vonalak hosszát a vonalszakaszok hosszainak összegzésével nyerik. A vonalszakaszok hosszát végpontjaik koordinátáiból a Pythagoras képlet felhasználásával számítják. Hasonlóképpen határozható meg a poligonok kerülete is annak figyelembevételével, hogy a kezdőpont koordinátái kétszer is szerepelnek a számításokban, mind az első, mind az utolsó egyenes szakasz hosszának meghatározásánál.

A térinformatikai szoftverek egyik leggyakrabban alkalmazott számítása a poligonok területének meghatározása. A számításhoz azt a geodéziában jól ismert algoritmust használják, mely a területet trapézok összegéből számítja.

2.41 ábra - poligon területszámítása

Ha a töréspontok számozása az óramutató járásával ellentétes, a területet negatív előjellel kapjuk. Mivel az y koordinátákból a középvonalak magasságát számítjuk, az algoritmus nem működik negatív ordináták esetén. Ebben az esetben két választásunk van: vagy az y tengelyre végezzük a vetítést, azaz a képletben az x-eket és y-okat felcseréljük (csak akkor alkalmazható eljárás, ha az x-ek pozitívok), vagy megfelelően nagy számmal megnöveljük az y értékeket, hogy eredményül pozitiv számokat kapjunk

Bocsájtsunk a poligon minden töréspontjából függőlegest az X tengelyre. Minden egyenes szakasz, a két végpontját levetítő egyenesekkel valamint az X tengely kimetszett részével egy egy trapézt alkot. Az i.-ik trapéz területe az alábbi képletből számítható:

Ha a poligon valamennyi oldalára elvégezzük a számítást és az eredményt összegezzük, úgy megkapjuk a poligon területét. Ez az egyesek számára talán váratlan eredmény abból adódik, hogy az alsó trapézok területe levonódik az összegből, mivel az óramutató járásával megegyező pontszámozás esetén, az (x_(i+1) - x_(i)) érték negatív. A poligon (zárt sokszög) területe tehát

A képlet használatakor figyelemmel kell lenni arra, hogy a poligon zártságából következően a kezdő és végpont koordinátái megegyeznek: (x_(n+1), y_(n+1))=(x_(i), y_(i)).

Az algoritmus tetszőleges alakú poligonra használható egy kivétellel: nem tudja kezelni azokat az eseteket amikor a poligon oldalak metsződnek (nyolcas alakot vesznek fel). Ebben az esetben ki kell számítani az oldalak metszéspontját, és ennek felhasználásával a poligont két poligonra kell bontani.

A gyakorlati feladatok során a poligonok általában folyamatosan boritják a felszínt (gondoljunk egy földmérési alaptérkép földrészleteire), és valamennyi poligon (földrészlet) területére szükség van. Ilyenkor célszerű az összes területet egyszerre számolni.

A program minden poligon számára létrehoz egy összegzőt és a poligon oldalakhoz számított területet a megfelelő poligon összegzőjében akkumulálja. A probléma azokkal az oldalakkal van, melyek egyidejűleg két poligonhoz is tartoznak. Ezeket a területeket ugyanis mind a két poligon összegzőjéhez hozzá kell adni, csak különböző előjellel. Ha továbbra is az óramutató járásának megfelelő haladási értelemmel számolunk, akkor a baloldali poligonok számára a részösszeg eredeti előjelével ellentétes, míg a jobboldali poligonok összegzői a részösszegeket előjelhelyesen kapják.

A térinformatikában gyakran használnak a terület típusú objektumok reprezentálására pontokat, bizonyos esetekben pld. a magyar geokód előírások figyelembevételekor a vonal típusú objektumok is képviselhetők ponttal. Bár a magyar előírások e pontok elhelyezésére többé kevésbé önkényesek (csak az a megkötés, hogy az objektum határvonalán vagy azon belül helyezkedjenek el), a szakmai igény megkívánja, hogy a képviselő pontok olyan egyértelmű és ismételhető szabálysorozat eredményeképpen kerüljenek meghatározásra, mely elhelyezkedésileg a lehető legjobban helyettesíti a képviselt objektumot. A terület tipusú objektumok ilyen helyettesítő pontjait centroidoknak hívjuk. Mivel a vonalas objektumok ponttal való helyettesítése a gyakorlatban kevéssé járható út, ezért a centroid fogalmát nem kívánjuk ezekre az objektumokra kiterjeszteni. Megjegyezzük ugyanakkor, hogy az azonosítást szolgáló pontok egyértelmű, szabályokkal leírt meghatározása ezeknél az objektumoknál is indokolt.

Terület típusú objektumok pontszerű helyettesítésére legalkalmasabb geometriai fogalom a súlypont. A súlyponti koordináták, meghatározás szerint az alábbi kifejezésekből nyerhetők:

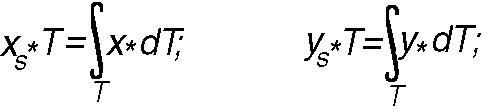
ahol (x_s, y_s) - a súlypont koordinátái, T - a síkidom területe, dT - infenitezimálisan kicsiny elemi terület, (x, y) az elemi terület sarokponti koordinátái. Az integrál jel alatti T azt jelképezi, hogy az integrálást az egész területre végre kell hajtani.

Poligonok esetében az általános képlet felhasználásával levezethető, hogy a súlyponti koordináták a poligon törésponti koordinátáinak és területének felhasználásával az alábbi kifejezésekből számíthatók:

Sajnos, amint ezt a 2.42 ábra is illusztrálja, konkáv poligonok esetén a súlypont az objektumon kívülre is eshet. Mivel egy objektumon kívüli pont nem játszhatja el a centroidtól elvárt funkciókat, ilyen esetben célszerű egyértelmű szabályt alkotni a súlypont objektumra történő visszavetítésére. A legegyszerűbb egyértelmű szabálynak az tűnik, ha a vetítés a legrövidebb távolság mentén történik a területi objektumra. A kérdéses centroid pont megkeresése érdekében kiszámítjuk a súlypont és a poligon töréspontok távolságait és kiválsztjuk közülük a legrövidebbet.

2.42 ábra - konkáv síkidom súlypontja az idomon kívül helyezkedik el

A centroid három helyzetet foglalhat el: vagy a súlypontból a kérdéses töréspontot megelőző oldalra bocsátott merőleges talppontjával lesz azonos, vagy a követő oldalra bocsátott merőleges talppontjával, vagy magával a törésponttal. Szimmetrikus területek esetén előfordulhat az a speciális eset, hogy a megelőző és követő oldalra bocsátott normálisok azonos hosszúságúak. Ebben az esetben, az egyértelműség biztosítása érdekében, a kisebb irányszögű normálist választjuk vetítősugárnak.

Legyen d_s-r=min{d_s,i}; i=1, 2, . . .n, akkor az r töréspontot megelőző oldal egyenlete

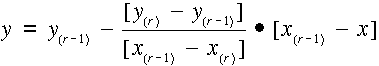
a súlypontból a megelőző oldalra bocsájtott merőlegesé pedig

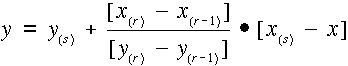
Ezután a metszési kifejezés felhasználásával kiszámítjuk a talppont (x_t-1, y_t-1) koordinátáit, a tartalmazási egyenlőtlenséggel pedig megvizsgáljuk, hogy rajta van-e az (r-1)-(r) egyenes szakaszon. A feltétel teljesülése esetén a súlyponti és talpponti koordinátákból Pythagoras képletével távolságot számolunk. Az eljárást megismételjük az (r)-(r+1) szakaszra is. Attól függően, hogy a talppontok a szakaszon belülre vagy kívülre esnek, maximum három, minimum egy távolságot kapunk. A legrövidebb távolsághoz tartozó végpont (valamelyik talppont, vagy az (r) töréspont) lesz az objektumot reprezentáló centroid.

Pont a poligonban algoritmus

A feladat mind egyes pontok, mind pontcsoportok vonatkozásában igen gyakran előfordul. Ha egyszerű példát akarunk mutatni erre a két esetre elég ha csak arra gondolunk, hogy minden pontszerű objektum valamilyen terület típusú objektumon belül helyezkedik el. Ha például arra vagyunk kíváncsiak, hogy egy forrás milyen földrészleten található, úgy ezt az algoritmust kell alkalmaznunk. De ezt az algoritmust igényli annak a kérdésnek a megválaszolása is, hogy hány centroiddal reprezentált épület található pld. a VI. kerületben.

Az algoritmus alapgondolatát már ismertettük, konverzió céljaira történő felhasználásával is foglalkoztunk. Most csak néhány olyan momentumra hívjuk fel a figyelmet, mely elősegíti az algoritmus gyakorlati realizálását. Az implementálás során annyiban módosítottuk a korrekten megfogalmazott algoritmust, hogy mivel a zérust nem tekintjük páratlan számnak, akkor van a pont a poligonban, ha a belőle kiinduló félegyenesnek páratlan számú metszéspontja van a poligont alkotó egyenes szakaszokkal, minden más esetben a pont a poligonon kívül van (azaz eltekintettünk a metszéspontok eggyel való megnövelésétől és az ebből fakadó paritáscserétől).

Húzzunk egy függőleges egyenest a pontból, keressük meg a metszéspontját a poligont alkotó egyenes szakaszokkal. Azért, hogy ne kelljen minden egyenessel kiszámítani a metszéspontot majd utána megnézni, hogy az a szakaszon belül vagy kívül van-e, már a metszéspont keresése előtt kirostáljuk a metszésre esélytelen vonalszakasz jelölteket az alábbiak szerint:
Legyenek a vizsgált pont koordinátái (u,v), az egyenes szakaszok kezdő és végponti koordinátáinak indexei pedig (i) és (i+1), a függőleges egyenesen x=u. Mivel a függőleges vonalszakaszok nem metsződnek a végesben a függőleges egyenesekkel, a vizsgálatot csak azokra a szakaszokra végezzük el melyekre igaz, hogy
x_(i+1)<>x_(i). A perspektív vonalszakaszok kiválasztását a [x_(i+1)-u]*[u-x_(i)]>=0 feltétel érvényesítése teszi lehetővé, ez ugyanis azt fejezi ki, hogy a vizsgált szakasz két végpontja a pont függőlegesétől jobbra illetve balra (esetleg az egyik végpont magán a függőlegesen) helyezkedik el.

Abban az esetben, ha a metszéspont x koordinátája egybeesik a vonalszakasz kezdő vagy végpontjával (a kezdő vagy végpont a vizsgált pont függőlegesében van) a metszéspont számlálás hibázhat. Ezt elkerülendő, két olyan feltételt iktatunk a programba, melyek azt biztosítják, hogy ha a metszéspont x_(i)-el esik egybe, úgy a program csak akkor számol metszéspontot, ha az (i+1)-es pont a függőlegestől jobbra esik, ha pedig x_(i+1) esik a pont függőlegesére, úgy a számlálás feltétele, hogy az (i).-ik pont a függőlegestől balra helyezkedjen el.

A metszéspont y koordinátáját megkapjuk, ha a kiválasztott egyenes szakasz egyenletébe behelyettesítjük az x=u értéket. Ha a metszéspont y koordinátája nagyobb mint v (a vizsgált pont y koordinátája), úgy a metszéspont a vizsgált pont fölött van, a számláló tartalmához hozzáadódik az egység és a vizsgálat mindaddig folytatódik, amíg a poligon összes oldala sorra nem kerül (legalább annak eldöntésére, hogy perspektív-e vagy sem).

A fentiekben vázolt program nem intézkedik külön arra az esetre, ha a vizsgált pont rajta van a poligon kerületén. Ez az eset egyszerűen figyelembe vehető azzal, hogy a számlálót akkor is beindítjuk, ha a metszéspont y koordinátája egyenlő v-el.

A gyakorlati esetekben több pont több poligonon belüli elhelyezkedését kell vizsgálni. A poligonok ezekben az esetekben, a topológiai adatmodell szerint, ívekben kerülnek tárolásra (két csomópont közötti egyenes szakaszok sorozata alkotja az ívet). Minden ív egyidejűleg két poligonhoz is tartozik. Mivel az ívek irányítottak, az érintett poligonokra baloldali és jobboldali jelzővel szokás hivatkozni.

Minden pontból kiindulva függőlegeseket húzunk és meghatározzuk a metszéspontok y koordinátáit. A kapott y értékeket együtt tároljuk a kérdéses ív alatti poligon nevével (Nyugatról-Keletre irányított poligonok esetén a jobboldali poligonéval). Valamennyi ív vizsgálata után meg kell keresni a legalsó metszéspontot és a hozzátartozó poligon nevét. Ez lesz az a poligon, amely a pontot tartalmazza. Az eljárást minden pontra elvégezve, megkapjuk minden pont tartalmazó poligonját. Az algoritmus igényli, hogy minden pontról minden ív vizsgálatra kerüljön. A vizsgálatok száma csökkenthető, ha az íveket előzetesen maximális és minimális x koordinátáiknak megfelelő csoportokba rendezzük, és az egyes pontokból csak azokat az íveket vizsgáljuk, melyek x szerinti intervalluma tartalmazza a figyelembe vett pont x értékét. Ezeken kívüli, y szerinti rendezésekkel tovább csökkenthető a megvizsgálandó ívek száma.