Mesterséges neurális hálóztok alkalmazása a térbeli interpolációban

Ebben a részben megismerkedünk

A mesterséges neurális hálózatok alapgondolatával, ezután bemutatjuk
az MLP hálózat működését, majd felvázoljuk a
feladatmegoldás menetét,
röviden utalunk néhány mesterséges neurális hálózatmodellező szoftverre, és
egy térbeli interpolációs alkalmazással fejezzük be a témát.

A következő pontot azért nem olvasztottam be az előző, skaláris terek modellezésével foglalkozó pontba, mivel ezzel is megpróbálom aláhúzni, ennek az új, számtalan területen használható technikának a jelentőségét.

Már itt utalok rá, hogy a módszer nem csak függvényterek interpolálására alkalmas, hanem osztályozásra is, ezt a tulajdonságát a Távérzékelés III fejezetben fogom felvázolni.

A módszer alkalmazási területei elvileg korlátlanok. Térbeli interpoláción kívül jó eredménnyel használják a beszéd és alakfelismerésben, robottechnikában, kódolásban és kódok megfejtésében, gépi fordításban, különböző osztályozási feladatokban, optimalizálásokban illetve piaci előrejelzésekben, sőt egyesek szerint a jövő számítógép hardverét is ezen az elven alapulva kell megkonstruálni.

Lássuk tehát a módszer lényegét anélkül, hogy belefeletkeznénk a különböző megoldó algoritmusok részleteibe. Ezt annál inkább megtehetjük, mivel szerencsére kiváló magyar nyelvű tankönyv [26] áll ebben a vadonatúj témában a részletek iránt érdeklődők rendelkezésére.

A mesterséges neurális hálózatok alapgondolata

Az emberi gondolkozás fiziológiájának kutatása során jutottak a kutatók arra a felismerésre, hogy a külvilág ingereit az érzékforrásokból az idegsejtek egy olyan bonyolult hálózaton továbbítják, mely kereszteződéseiben lévő csomópontok a különböző összeköttetésekből érkező információt feldolgozzák és a feldolgozott értékeket számtalan további idegszálon keresztül újabb csomópontok felé továbbítják, míg el nem érik a kérdéses ingerre adandó válaszért felelős agyi egységeket. Az aktív csomópontokat a kutatók perceptronnak nevezték el.

Hogy a számtalan részfeldolgozáson átesett inger milyen választ vált ki az részben örökletes tényezőktől függ, részben pedig az egyén tapasztalatától illetve a tanulástól. Ez más szóval azt jelenti, hogy bizonyos bemeneti hatásokra a rendszer 'behuzalozottan' (előre programozottan) működik, míg más bemeneti adatok esetén a válasz függ az egyén tapasztalataitól, korától iskolai végzettségétől, stb. A nem orvosi kutatások szempontjából az a lényeges, hogy ez a struktúra adaptív azaz válaszával képes a bemeneti adatokhoz tanulással alkalmazkodni.

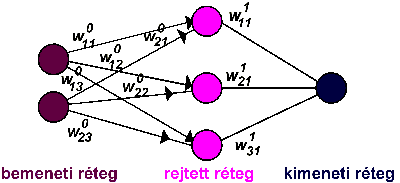
2.59 ábra - MLP hálózat vázlata

A 2.59 ábrán felvázoltunk egy egyszerű MLP típusú mesterséges neurális hálózatot. Az MLP (Multi Layer Perceptron) típust a mesterséges neurális hálózatok alapértelmezésének tekinthetjük. Különösen osztályozási feladatokra más hálózatok is ismertek, pld. a Kohonen féle vagy az Önszerveződő Térképek típusú, ezekre majd a távérzékelési fejezetben utalunk.

Az MLP hálózatban három réteg típussal találkozunk. A bemenő réteg annyi elemből (neuronból) áll ahány bemenő változónk van (az ábrán látható példában két bemenő változó szerepel). Rejtettrétegből, elvileg tetszőleges számú lehet, és minden rejtett réteg elvileg tetszés szerinti számú neuront tartalmazhat (rajzunkon egy rejtett réteg szerepel három neuronnal). Kimeneti rétegből mindig egy van, annyi neuronnal ahány kimeneti változónk van (példánkban egy).

Alapértelmezésben egy adott réteg minden csomópontja össze van kötve a következő, tehát tőle jobbra eső réteg minden csomópontjával.

Ez alól a szabály alól két kivétel fordulhat elő:

az idősorok elemzésére alkalmazott hálózatokban különböző típusú visszacsatolásokat alkalmaznak. Ezek közül az a legegyszerűbb ha a t időponthoz tartozó kimenetet azonosnak tekintik a t+1 időponthoz tartozó bemenettel;

· a szabályos MLP hálózatokban tanításuk után nem feltétlenül minden összeköttetés vesz aktívan részt a kimenet létrehozásában, s azért hogy a felesleges számításokat elkerüljék kidolgoztak olyan algoritmusokat, melyek segítségével adott adatrendszerhez csökkenteni lehet az összeköttetések számát.

Az MLP hálózat működése

Ahhoz hogy megértsük a hálózat működését, először azt kell felvázolnunk, hogy mit is várunk el a hálózattól.

Tételezzük fel, hogy megmérjük egy tó szennyezettségét arányosan elosztva több pontban. Ismerjük a mérési pontok x, y koordinátáit valamint a víz felszínétől számított mélységüket. Ugyanezekben a pontokban ismerjük a tó teljes mélységét is. Arra vagyunk kíváncsiak, hogy olyan pontokban ahol nem mértünk szennyezettséget de (szintvonalas térképről) ismerjük a tó mélységét, tehát adott x, y, felszíntől mért távolság és teljes mélység esetén mennyi lesz a szennyezettség értéke?

Ahhoz hogy ilyen vagy hasonló feladatokra választ kaphassunk először a hálózatot tanítani (train) kell. A tréning abból áll, hogy ismert bemenő adatokból a hálózat működési eredményét (kimenetét) ismert adatokhoz (úgynevezett cél adatokhoz) hasonlítjuk, és ha a mennyiségek eltérnek, úgy igazítjuk a hálózat működését, hogy az eltérés minél gyorsabban eltűnjön.

Az előző bekezdés több kérdést is felvet, mindenek előtt azt, hogy mit értünk a hálózat működésén.

A hálózat minden összeköttetéséhez rendeltünk egy w_ij^r alakú súlyt, ahol r a réteg sorszáma, i és j pedig az irány kezdő és végpontját jelölő neuronok sorszáma rétegükön belül (a rajzon a zsúfoltság elkerülése érdekében a rétegekre és neuronokra a számokat nem írtuk ki).

A bemenő jel megszorzódik a kérdéses irányhoz tartozó súllyal majd belép az irány végén lévő neuronba. A neuronba belépő értékek összegződnek majd az összeget egy transzformáló függvény átalakítja és a következő összeköttetésekre adja, ahol megszorzódnak az irányokhoz tartozó súlyokkal. A folyamat mindaddig folytatódik míg el nem érik a kimeneti neuron(oka)t.

Mit lehet változtatni ezen a hálózaton a célból, hogy a kimenet közeledjen az ismert értékekhez az úgynevezett cél adatokhoz? Természetesen a w_ij^r súlyokat. Erre szolgál a backpropagation (visszaterjesztés) nevű algoritmus számtalan változata.

Nem szóltunk még arról, hogy milyen transzformáló függvényeket alkalmaznak. Jobbra dűlt S betűre hasonlít a szigmoid (néha logisztikusnak is hívják), képlete: . A függvény értékei 0 és 1 közt változnak, ha s=0, y=0.5.

A másik gyakran használt függvény a tangens hiperbolicus, képlete . Kimeneti értékei -1 és +1 között változnak, ha s=0, y=0.

Újabban egyre népszerűbb a Gauss féle aktiváló függvény: . Ennek a kimenetei is 0 és 1 között változnak, ha s=0, y=1. A függvények MATHCAD-ban készült rajzait D=1 és D=1.5 esetére 2.60 ábrán tüntettük fel. Figyeljük meg, hogy a 'hasznos' bemeneti értékek, azaz amelyek más bemenethez más kimenetet rendelnek a D értékétől függően kb. 4 és 2.7 között helyezkednek el.

A fenti függvényeket, esetenként keverten is, a rejtett rétegek neuronjaiban alkalmazzák, a bemenő neuronokban nincs transzformáló elem csak súlyok, a kimenő neuronok pedig rendszerint lineáris transzformációt alkalmaznak.

Amint látjuk az aktiváló függvények kimenetei -1, +1, illetve 0, +1 tartományokban működnek, mely értékeket a D-től függően 2.7-4 körüli bemeneti értéknél érik el, ami azt jelenti, hogy ha a bemenetre abszolút értékre nagyobb számokat adunk (pld 5-öt és 6-ot) a rendszer kimenete lényegében azonos lesz, más szavakkal a bemenet változására a rendszer érzéketlen lesz és a tanulási folyamat lassú lesz és nem fog konvergálni.

Ezt elkerülendő a bemenő adatokat normálni szokták. Ez azt jelenti, hogy minden bemenő adat vektorra (vagy egyszerűen adatoszlopra) elvégzik a következő műveletet: kivonják minden adatból az oszlop középértékét, majd az így kapott számokat elosztják az oszlop szórásával s-val (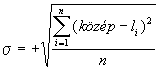) . A szórás helyett más számmal is oszthatnak a lényeg hogy a normált bemenő adatok az aktiváló függvény hatásos szakaszára essenek.

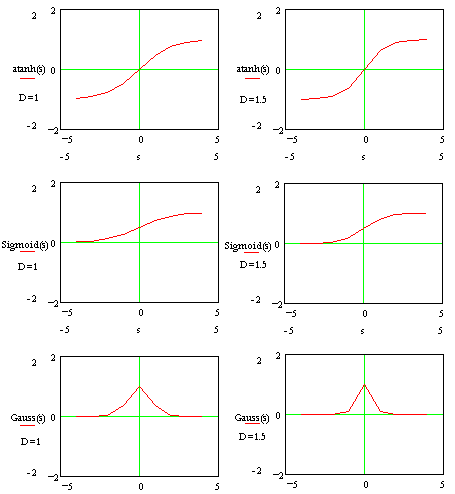
2.60 ábra - neuron aktiváló függvények

Ha a kimeneti neuronok lineáris aktiváló függvényűek úgy a kimenetet nem kell skálázni, bár ha a kimeneti értékek túl nagyok numerikus megfontolások ezt is indokolhatják.

A feladatmegoldás menete

Függetlenül attól, hogy milyen szoftvert használunk a feladatmegoldás a következő fő lépésekből áll:

a tanuló adatok összeállítása

kiválasztjuk a rendelkezésünkre álló ismert bemenő adat - eredmény (céladat) rekordokat (sorokat) és rendszerint valamilyen vesszővel, tabulátorral vagy space-szel elválasztott formátumú ASCII file-t szerkesztünk belőlük valamilyen text editorban vagy táblázatkezelőben (pld.EXCELL). A file-ok fejezetében (az első sorban), a szoftvertől függő módon, meg kell adni, hogy mely oszlopok bemenő adatok és mely oszlopok kimenő (cél) adatok.

2. a teszt adatok összeállítása

ha maradtak ismert bemenő adat - kimenő adat rekordok, melyeket nem használtunk a tréning fájlban, úgy ezekből a tréning adat fájlhoz hasonló formátumú teszt adatfájlt hozhatunk létre. A teszt adatok nem javítják a súlyokat, 'csak' tájékoztatják a felhasználót arról, hogy mennyire jól tervezte meg a hálózatát - elfogadhatók-e az eredmények vagy új tréningre (más módszerrel, más induló értékekkel) esetleg új hálózatra van szükség.

3. a hálózat megtervezése

a trénig fájl létrehozásával már megterveztük a bemenő és kimenő rétegben található neuronok számát. Ezután már 'csak' azt kel megterveznünk, hogy hány rejtett rétegünk lesz, hány neuron lesz az egyes rétegekben és milyen aktiváló függvényeket alkalmazunk a rejtett rétegek neuronjaiban (feltételeztük, hogy a kimenő réteg neuronjai lineáris aktiváló függvényekkel rendelkeznek).

Sajnos a hálózati elemek számának megbecsülésére eléggé ellentmondásos irodalmi adatokkal találkozunk. Közismert az az állítás, hogy legalább annyi sornak (összetartozó ismert be és kimenő adatnak) kell lenni a tréning adatfájlban ahány súly van a hálózatban. Ezt a tételt azonban egyesek explicit, mások implicit módon cáfolják. Az explicit cáfolat tapasztalati alapon bizonyítja, hogy bizonyos esetekben olyan hálózatok is kiválóan működnek, melyeknek sokkal több súlya van mint ahány tréning sora. Az implicit cáfolat azokban a tételekben és javaslatokban fogalmazódik meg, melyek azt mondják, hogy a legtöbb folytonos függvény közelíthető olyan hálózattal, mely kimenő neuronjai lineárisak, egy rejtett rétege pedig N-1 neuront tartalmaz ahol N a tréning adatok száma. Nem nehéz kimutatni az ellentmondást az előző vastagbetűs állítás és e között, hisz például egy 1 bemenettel, 1 kimenettel és 6 rejtett rétegbeli neuronnal rendelkező hálózatnak 12 súlya van. Egy harmadik állítás szerint a két rejtett rétegű hálózatban N/2+3 rejtett neuron elég a folytonos függvények approximálására. Ez pedig 1 bemenet 1 kimenet és két rétegben elhelyezett 4-4 neuron esetén 24 súlyt jelent míg N=10.

Hogy mégis adjunk valamilyen fogódzkodót azt javasoljuk, hogy minél több tréning adatot használjunk, az első kísérletben próbáljuk ki a két réteges megoldást az N/2+3 számú neuronnal, nem kellő konvergencia esetén növeljük a rétegek számát a nélkül, hogy a rejtett neuronok számát növelnénk.

Az igazi megoldást azok az algoritmusok szolgáltatják, melyek a célfüggvény optimális kielégítését vagy az egy rétegen belüli neuronok számának automatikus növelésével érik el mint a Scott Fahlman féle cascad correláció, vagy a rétegeket is meg az elemeket is automatikusan növelik mint a flexnet algoritmus. Ez utóbbi esetében arra is van lehetőség, hogy a létrehozott topológiát tovább tanítsuk valamely backpropagation tanító eljárással.

A hálózat megtervezéséhez tartozik az aktiváló függvények megválasztása is. Bár itt sem lehet általános szabályokat megfogalmazni, az irodalom szerint nem túl zajos adatoknál előnyös az arccth, míg zajos adatoknál a Gauss függvény alkalmazása.

4. a hálózat tanítása

mielőtt a tanítási folyamatot elindítjuk gondoskodni kell arról, hogy a bemenő adatok és esetleg a kimenő adatok skálázása is megtörténjen. Erre rendszerint egy előfeldolgozási szakaszban kerül sor.

Ezután meg kell választanunk a tanítási módszert, a tanulási sebesség és nyomaték értékét, a kezdeti súlyinicializálás módszerét és a megállási kritériumot (csak a legfontosabb vezérlő beállításokat soroltuk fel, a programok más dolgokat is kérhetnek). Számtalan backpropagation tanulási módszer létezik, ezek közül, sebessége alapján, a quickpropagation használatát javasolhatom. A korszerű algoritmusok lehetővé teszik, hogy a tanulási sebesség és nyomaték a szükségletnek megfelelően automatikusan változzon a tanulási folyamatban. A súlyinicializálást a jobb szoftverek automatikusan végzik, ha nem, be kell adni nekik egy véletlen számot. Igen lényeges, hogy a megállási kritériumra szigorú feltételeket szabjunk, ugyanis a megengedett középhiba értékénél figyelembe kell vennünk a skálázást is.

Fel kell készülnünk arra, hogy egy bonyolultabb hálózat tanítása gyors számítógépen is több órát sőt napot is igénybe vehet. Nem véletlenül futnak az igazán professzionális programcsomagok még ma is csak a UNIX platformokon.

5. Az eredmények meghatározása

Bár az egész munkát ezért csináljuk, sajnos erről se az irodalom se a szoftverek kézikönyvei sem igazán írnak. A tanított hálózat végső súlyait elmentjük és ezekkel a súlyokkal a korábbi hálózati topológia alapján kiszámíttatjuk az ismeretlen bemeneti értékekhez tartozó kimeneteket. Ez a számítás gyakorlatilag pillanatok alatt kész van. Következésképpen ha a jelenség amit modelleztünk állandó (pld egy kód vagy nyelv) és korlátos is úgy a súlyokat bármikor újabb tanítás nélkül felhasználhatjuk az eredmények meghatározására. Ha a jelenség állandó de igen bonyolult (pld. a terepfelszín), úgy újabb mérési adatok előfordulása esetén újra taníthatjuk a hálózatot, de kiinduló adatként a már korábban meghatározott súlyokat alkalmazva jelentősen lerövidített idő alatt tudjuk a tanítást végrehajtani.

A legproblematikusabbak a folyamatosan változó jelenségek modellezése, ezeknél gyakran kell a hálózatokat újra tanítani.

Mesterséges neurális hálózati szoftverek

Amint erről már szóltunk a legtöbb szoftver munkaállomásokon fut UNIX operációs rendszer alatt. A szoftverek jelentős része kereskedelmi és igen drága, de szerencsére még elég sok egyetemi kutatóhely ingyen bocsátja a felhasználók rendelkezésére szoftverét.

A szabad szoftverek többsége szintén csak UNIXalatt fut, de több letölthető forrásnyelven is (rendszerint C++-ban, de újabban néhány JAVA forrás is megjelent), illetve néhány MS DOS és WINDOWS 95-ös verzióval is találkozunk. Sajnos a DOS exe fájlok kompillálása nem mindig sikeres pld. a NevProp3 nevű program DOS exéje minden eddig kipróbált adatállománnyal 'elszállt', a következő bekezdésben javasolt FAST programnak pedig a cascade 2 modulja hoz létre rendszer hibát.

A szabad szoftverek közül kettőre hívjuk fel az olvasó figyelmét, megadva azokat az INTERNET címeket, ahonnan letölthetőek.

Először a már idézett FAST 2.2 szoftvert említem, mely oktatási változata különbőző platformokra egy idejig letölthető volt a http://www.forwiss.uni-erlangen.de/aknn/Projekte/FAST/ACADEMIC/ könyvtárból. Aki a teljes verzió iránt érdeklődik az intézménye megnevezésével és tevékenységi köre leírásával írjon a következő címre: kindermann@forwiss.uni-erlangen.de. Mivel én csak a szabad 'akadémiai' verziót ismerem az a két hiba amit észrevettem a teljes verzióban valószínűleg nem fordul elő, különösen akkor, ha a fordítást C-ből magunk végezzük a saját gépünkre installált kompájlerrel.

Az első hibát már említettük a cascade 2 modullal kapcsolatban. A következő hiba vagy inkább korlátozás, hogy a hibahatárok alapértelmezett értékeit nem lehet megváltoztatni. Sajnos ez a korlátozás lehetetlenné teheti sok interpolálási feladat megoldását. A szoftver számos előnye közül számomra talán az a legfontosabb, hogy a flex modul automatikusan megtervezi a többrétegű hálózatot, a cascor modul pedig egy rejtett réteget tervezve oldja meg a feladatot (sajnos ez a nagyon gyors modul szinte rögtön leáll az alapértelmezésként megadott igen nagy, 0.1 értékű hibaküszöb miatt).

A második szabad program a Stuttgarti Neurális Hálózat Szimulátor vagy eredeti nevén SNNS 4.1 verziója, melynek 1998 eljére készült el windows95/NT-variánsa, mely letölthető a következő ftp címről: ftp://ftp.informatik.uni-stuttgart.de/pub/SNNS/SNNSV4.1-win32/.

A windowsos változat problémája, hogy az MS Windows-hoz készült X-Server programot igényel. Ezek a programok általában nem ingyenesek, a mellékelt Startnet Micro X-Win32 X-Server Demo szabad formájában bizonyos korlátozásokkal használható csak, egy másik szabad X-Serever az alábbi címről tölthető le: http://tnt.microimages.com/www/html/freestuf/mix/

Sajnos az SNNS-et még nem tudtam térinformatikai feladatra kipróbálni, mivel eddig csak UNIX alatt futott, a különböző szoftver ismertetők azonban nagyon dicsérték, remélhetőleg érdemes lesz tesztelni.

Az Interneten nagyon sok shareware illetve freeware software található, a shareware-k szinte minden esetben annyira korlátozottak, hogy csak demónak használhatók, a szabad szoftverek pedig rendszerint UNIX-ra iródtak, vagy csak forrásnyelven tölthetők le. Hogy a kompillálási problémák ne zavarják a neurális hálózatok tanulmányozását úgy gondolom, hogy az első próbálkozásokhoz ez a két szoftver elég lesz, utána pedig mindenki szabadon kereshet magának megfelelőbbet.

Térbeli interpolálási példa

Az irodalom nem bővelkedik közleményekben a mesterséges neurális hálózatok térbeli interpolációra történő felhasználásáról. Az ismertetendő kutatás [27] az 1997 októberi GIS/LIS '97 konferencián hangzott el az OHIO állambeli Cincinnatiban.

A kutatás célja Délkarolina állam havi csapadékadatainak interpolálása volt. A tréning adatokat 50 csapadékmérő állomás adatai szolgáltatták, míg az interpolációt 18 tulajdonképpen szintén ismert tesztállomásra végezték. Ebből is látszik, hogy kutatásról van szó, ezért kellett oda interpolálni, ahol már ismert adatok álltak rendelkezésre.

Az interpolációt még négy másik módszerrel is elvégezték, a kontrol módszerek a következők voltak: voronoi cellák, inverz távolság, polinómos interpoláció (trend felület) és krígelés.

A létrehozott neurális hálózat három rétegből állt: a bemenő rétegnek kilenc neuronja volt, az egyetlen rejtett réteget tíz neuron alkotta, a kimenő rétegben egy neuron helyezkedett el.

Igen érdekes a bemenő adatok megválasztása. Az interpolációt három, a vizsgált helyhez legközelebb fekvő esőmérő állomás adataira támaszkodva végezték olymódon, hogy bemenő adatként nem csak az állomások havi csapadék adatait, hanem a vizsgálati helytől mért távolságukat illetve tengerszínt feletti magasságukat is szerepeltették.

Számomra nem teljesen világos, hogy miért nem szerepelt a bemenő adatok között magának a keresett helynek a magassága, esetleg vízszintes koordinátái.

A magasság és távolság értékeket a 0, 1 tartományba transzformálták. A tréninget a konjugált grádiens módszerrel végezték, a megállás feltétele az volt, hogy a tréning adatok négyzetes középhibája csökkenjen le 0.01 értékre.

A vizsgálat végeredményeképpen megállapították, hogy a neurális hálózatokkal végzett interpoláció minden hónapra megbízható értéket szolgáltatott, míg a többi módszer egy egy hónapban ugyan jobb eredményt nyújtott, de átlagos teljesítményük elmaradt a neurális hálózati interpoláció mögött.

A példa igen jól illusztrálja, hogy a a hálózat megtervezésére megadott szabályok a tréning adatok és a hálózati súlyok illetve rejtett neuronok száma között nem feltétlenül érvényesülnek a valós hálózatokban. Esetünkben 100 súly van azaz az első szabály szerint 100 tréning adatra volna szükségünk, szemben a ténylegesen meglévő 50-el. A második szabály szerint viszont az egyetlen rejtett rétegben 49 neuronnak kéne lenni ahhoz, hogy a legtöbb folytonos függvényt le tudja képezni 50 tréning adat esetére a hálózat. Persze ez nem zárja ki, hogy a példában szereplő függvény kevesebb neuronnal is leképezhető.

A legtöbb szerző nyomatékosan javasolja a bemenő adatok számának csökkentését. Esetünkben például elképzelhetőnek tartom, hogy a bemenő adatokként x, y, z koordinátákat válasszunk (x, y esetében természetesen súlyponti koordinátákra gondolok), s ugyanakkor növeljük a tréning adatok számát. Ezzel olyan általános szabályt dolgozunk ki, mely nem csak Délkarolinára lesz igaz, hanem arra az egész területre, melyet a tréning adatok behálóznak.

Végső konklúzióként megállapíthatjuk, hogy még csak az elején vagyunk a neurális hálózatok térinformatikai hasznosításának, és még sok kutatást kell végezni ahhoz, hogy ezt az eszközt is beilleszthessük a sztenderd térinformatikai függvények tárházába.